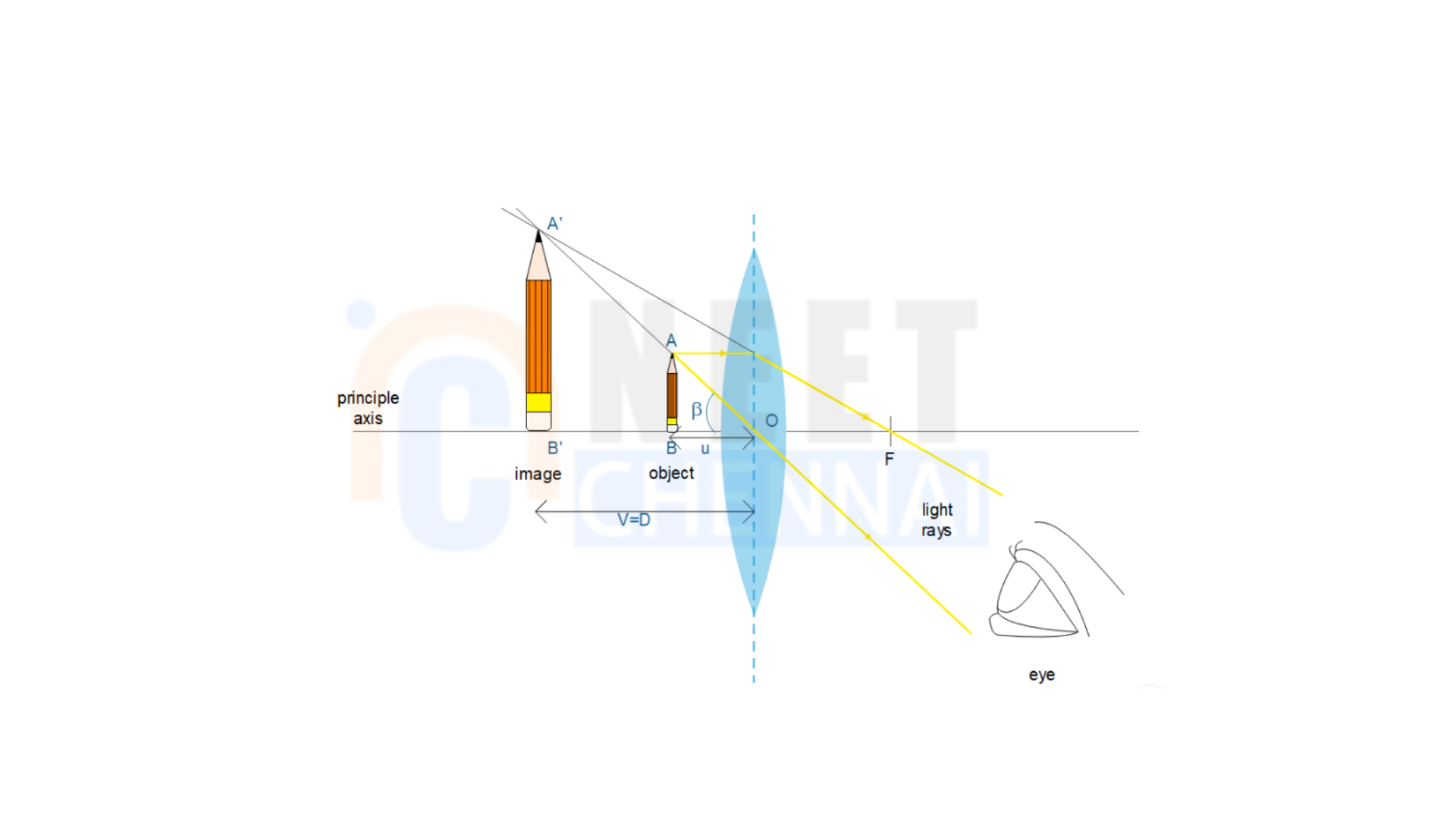
Explain simple microscope on the basis of the following points:
(a) Ray diagram for the formation of image;
(b) Expression for magnifying power when the final image is formed:
(i) At the least distance of distinct vision;
(ii) At infinity.
Hint:A simple microscope uses a convex lens to produce a magnified, virtual, and upright image at the distance of distinct vision (DDV). In a convex lens, this is achieved when the object is within the focal length of the lens. Magnifying power is defined as the ratio of the angle made by the image at the eye to the angle made by the object seen with the unaided eye at DDV. By applying this concept to the formula for magnifying power, we can find expressions for both cases—when the image is at DDV and when it’s at infinity.
Solution:
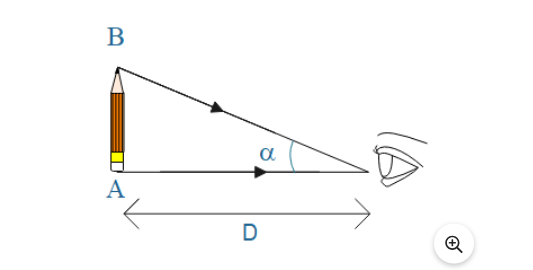

The magnifying power (M.P.) of a simple microscope is the ratio of the angle \(\beta\) (angle made at the eye by the image) to the angle \(\alpha\) (angle made at the eye by the object placed at DDV), given by:
\(\text{M.P.} = \frac{\text{Angle subtended by the image at the eye}}{\text{Angle subtended by the object at DDV}} = \frac{\beta}{\alpha}\)
For small angles, we can approximate:
\(\tan \beta \approx \beta = \frac{AB}{u}\)
and
\(\tan \alpha \approx \alpha = \frac{AB}{D}\)
where \(AB\) is the height of the object, \(u\) is the object distance, and \(D\) is the distance of distinct vision.
Substitute these values:
\(\text{M.P.} = \frac{AB / u}{AB / D} = \frac{D}{u}\)
From the lens formula:
\(\frac{1}{v} – \frac{1}{u} = \frac{1}{f}\)
where \(f\) is the focal length of the lens. Using sign conventions, with \(u\) and \(v\) as negative for a virtual image, we get:
\(\frac{1}{u} = \frac{1}{v} + \frac{1}{f}\)
thus:
\(\frac{D}{u} = \frac{D}{v + D / f}\)
This leads us to the magnifying power formula for a simple microscope.
Case (i): Image at the Distance of Distinct Vision (DDV)
If the image forms at DDV, where \(v = D\):
\(\text{M.P.} = \left(1 + \frac{D}{f}\right)\)
So, when the image is at DDV, the magnifying power is \(1 + \frac{D}{f}\).
Case (ii): Image at Infinity
If the image forms at infinity (\(v = \infty\)):
\(\text{M.P.} = \frac{D}{f}\)
Thus, the magnifying power is \(\frac{D}{f}\) when the image forms at infinity.
Note:
From these cases, we can conclude that the magnifying power of a simple microscope is between \(\frac{D}{f} \) and \( 1 + \frac{D}{f}\). The magnifying power is inversely proportional to the focal length of the lens, reaching its maximum when the image forms at DDV.