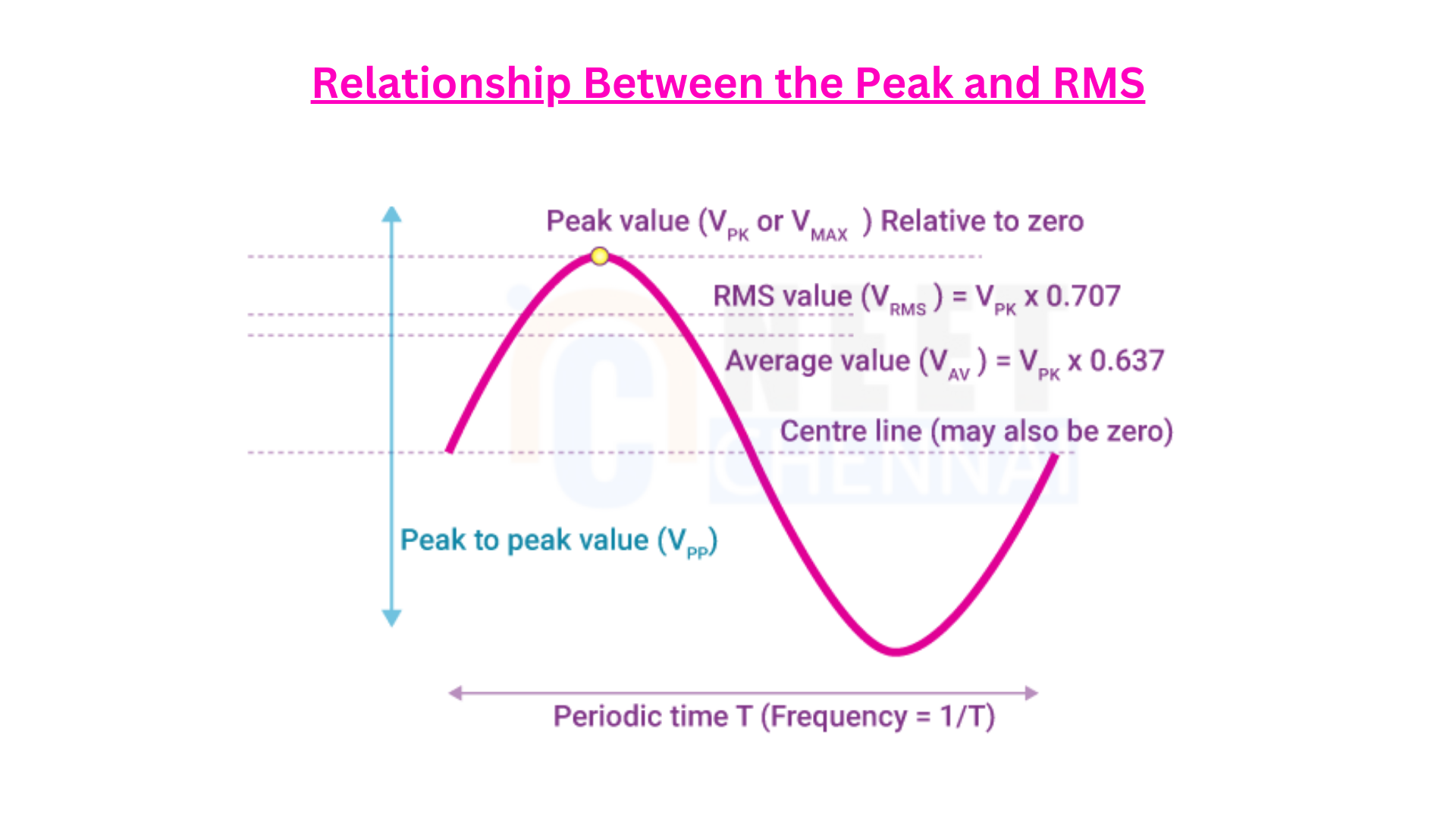
Derive the relationship between the peak and the rms value of current in an a.c. circuit.
Hint: In an AC circuit, the current is called alternating current (AC), which means it changes magnitude over time and periodically reverses direction. To find the relationship between the root mean square (rms) value and peak value of the current, we can start with a general equation for current and use the rms current formula.
Solution:
The current in an AC circuit can be represented by:
\(I = I_0 \sin(\omega t)\)
where \(I_0\) is the peak (maximum) value of the current.
The heat generated in the circuit is given by:
\(dH = I^2 R \, dt\)
Substituting \(I = I_0 \sin(\omega t)\) into this equation:
\(dH = (I_0 \sin(\omega t))^2 R \, dt\)
\(dH = I_0^2 R \sin^2(\omega t) \, dt\)
To find the total heat produced over half a cycle (from \( 0 to T/2\), where \(T\) is the period), we integrate:
\(H = \int_0^{T/2} I_0^2 R \sin^2(\omega t) \, dt\)
Using the identity \(\sin^2(\omega t) = \frac{1 – \cos(2\omega t)}{2}\):
\(H = I_0^2 R \int_0^{T/2} \frac{1 – \cos(2\omega t)}{2} \, dt\)
\(H = \frac{I_0^2 R}{2} \int_0^{T/2} (1 – \cos(2\omega t)) \, dt\)
Evaluating the integral:
\(H = \frac{I_0^2 R}{2} \cdot \frac{T}{2}\)
\(H = \frac{I_0^2 R T}{4}\)
The rms current, \(I_{\text{rms}}\), is defined by the heat dissipated in terms of rms current:
\(H = I_{\text{rms}}^2 R \cdot \frac{T}{2}\)
Setting these expressions for \(H\) equal to each other:
\(I_{\text{rms}}^2 R \cdot \frac{T}{2} = \frac{I_0^2 R T}{4}\)
\(I_{\text{rms}}^2 = \frac{I_0^2}{2}\)
\(I_{\text{rms}} = \frac{I_0}{\sqrt{2}}\)
Thus:
\(I_{\text{rms}} = 0.707 I_0\)
Conclusion: The relationship between the peak current \(I_0\) and the rms current \(I_{\text{rms}}\) in an AC circuit is:
\(I_{\text{rms}} = 0.707 I_0\)
Note: The peak current represents the highest value in one cycle, while the rms current (root mean square) is the effective current that would produce the same heat in a resistor as a direct current (DC) of that value. Here, we used the heat dissipation equations for both the peak and rms currents to derive this relationship.