Packing fraction in face centered cubic unit cell is:
(A) 0.7406
(B) 0.6802
(C) 0.5236
(D) None of the above
Hint: To improve understanding, it’s essential to know what packing fraction is. Packing fraction represents the variation between the isotopic mass and the total mass number (atomic mass). This fraction can be positive or negative, depending on the mass converted to energy during nucleus formation.
Complete step by step solution:
Let us know what is face centered cubic unit cell and then solve for its packing fraction:
Packing faction or Packing efficiency is the percentage of total space filled by the particles.
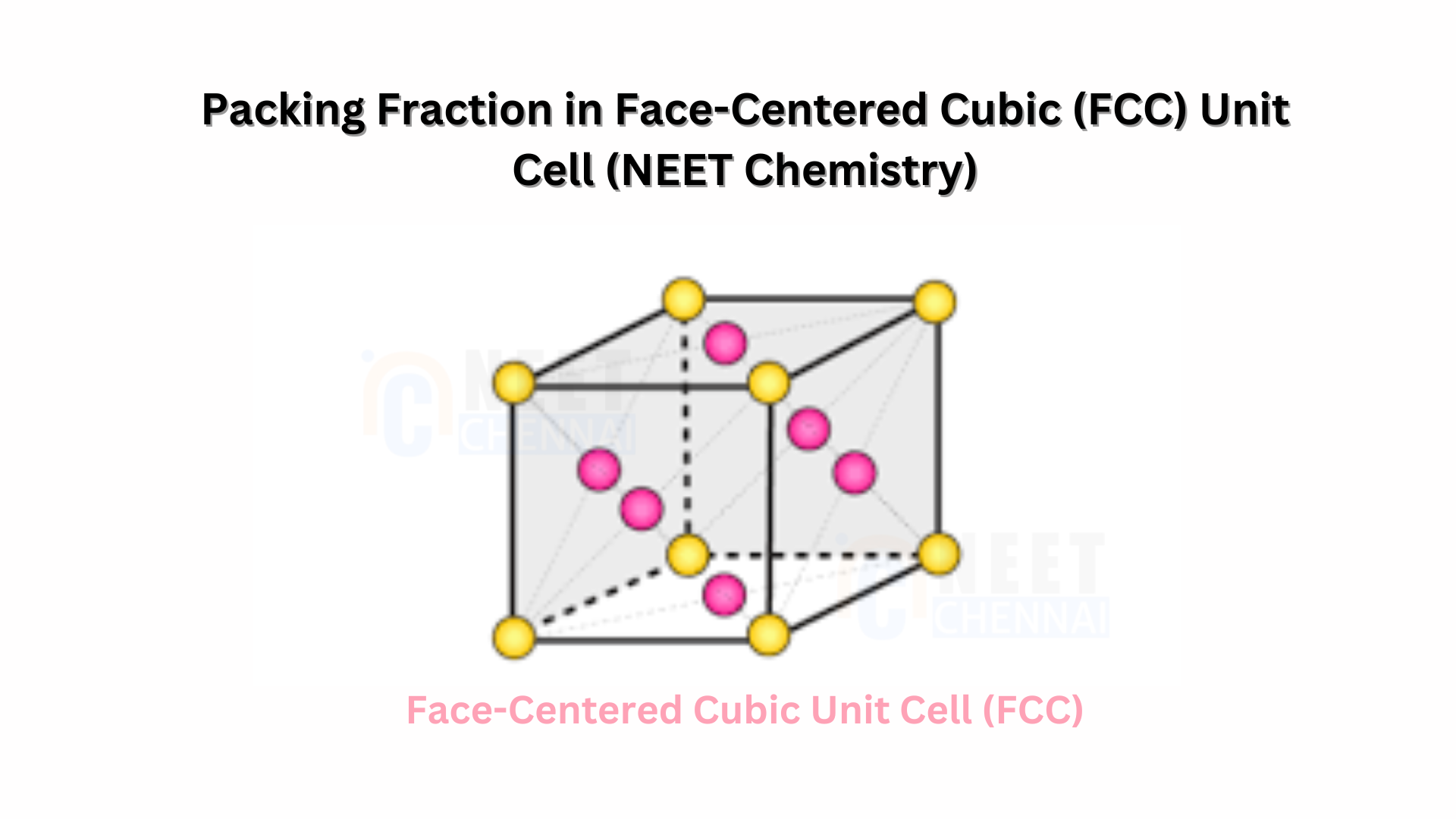
The face centered unit cell (FCC) contains atoms at all the corners of the crystal lattice and at the center of all the faces of the cube. The atom present at the face centered is shared between 2 adjacent unit cells and only 1/2 of each atom belongs to an individual cell. The packing efficiency of FCC lattice is 74%.
Let r be the radius of the sphere and a be the edge length of the cube and the number of atoms or spheres is n that is equal to 4. As there are 4 sphere in FCC unit cell
Volume of four spheres is given by
\( V = 4 \times \frac{4}{3} \pi r^3 \)In FCC, the corner spheres are in touch with the face centered sphere so the relation between the edge length and radius of the sphere is given by
\( r = \frac{a}{2\sqrt{2}} \)Substituting the above values in the below equation and solving:
\( { \Large Packing efficiency} = \frac{\text{Volume occupied by all the spheres in unit cell}}{\text{Total volume of the unit cell}} \times 100 \)
\( { \Large Packing fraction} = \frac{n \times \frac{4}{3} \pi r^3}{a^3} \) \( {\Large Packing fraction} = \frac{4 \times \frac{4}{3} \times \left(\frac{a}{2\sqrt{2}}\right)^3}{a^3} = \frac{\pi}{3\sqrt{2}} = 0.74 \)Hence the correct option is (A).
Note: The connection between the edge length of a cubic unit cell and the radius of the sphere can be accurately determined using diagrams and mathematical principles. The packing efficiency of various cubic unit cells differs based on their structure and geometry.