How will you obtain OR, AND gates from the NAND and NOR gates? Write symbols, Boolean formula, and truth table.
Hint: When we connect the inputs of a NAND gate together, we create a NOT gate. Similarly, by joining the two inputs of a NOR gate, we can also obtain a NOT gate. Formula used: In this explanation, we will utilize the following formula:
NOT(A)=\(\overline{A}\) where A is an input.
OR(AB)=A+B,signifies the OR gates acting on input A and B,
AND(AB)=A⋅B, AND signifies the AND gates acting on input A and B
Complete answer:
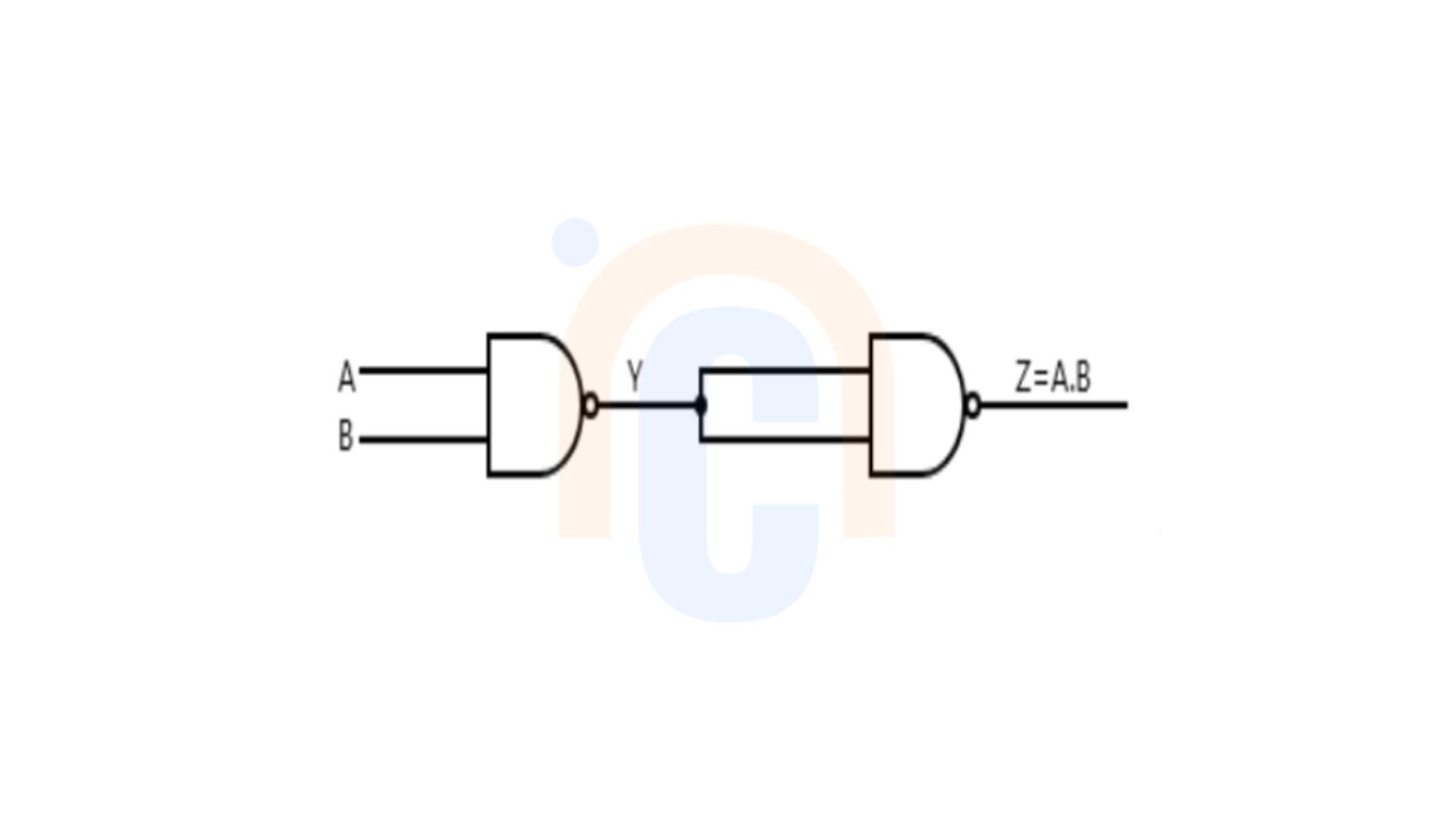
To obtain an AND gate from NAND gates, we first feed the inputs A and B into the NAND gates.
When the output is sent into another NAND gate with both inputs connected together, it produces an output Z,
Boolean formula: Z=\(\overline{Y}\)=\(\overline{\overline{A \cdot B}} = A \cdot B\)
|
A |
B | Y | Z |
|
0 |
0 | 1 | 0 |
|
1 |
0 | 1 | 0 |
|
0 |
1 | 1 | 0 |
| 1 | 0 | 0 |
1 |
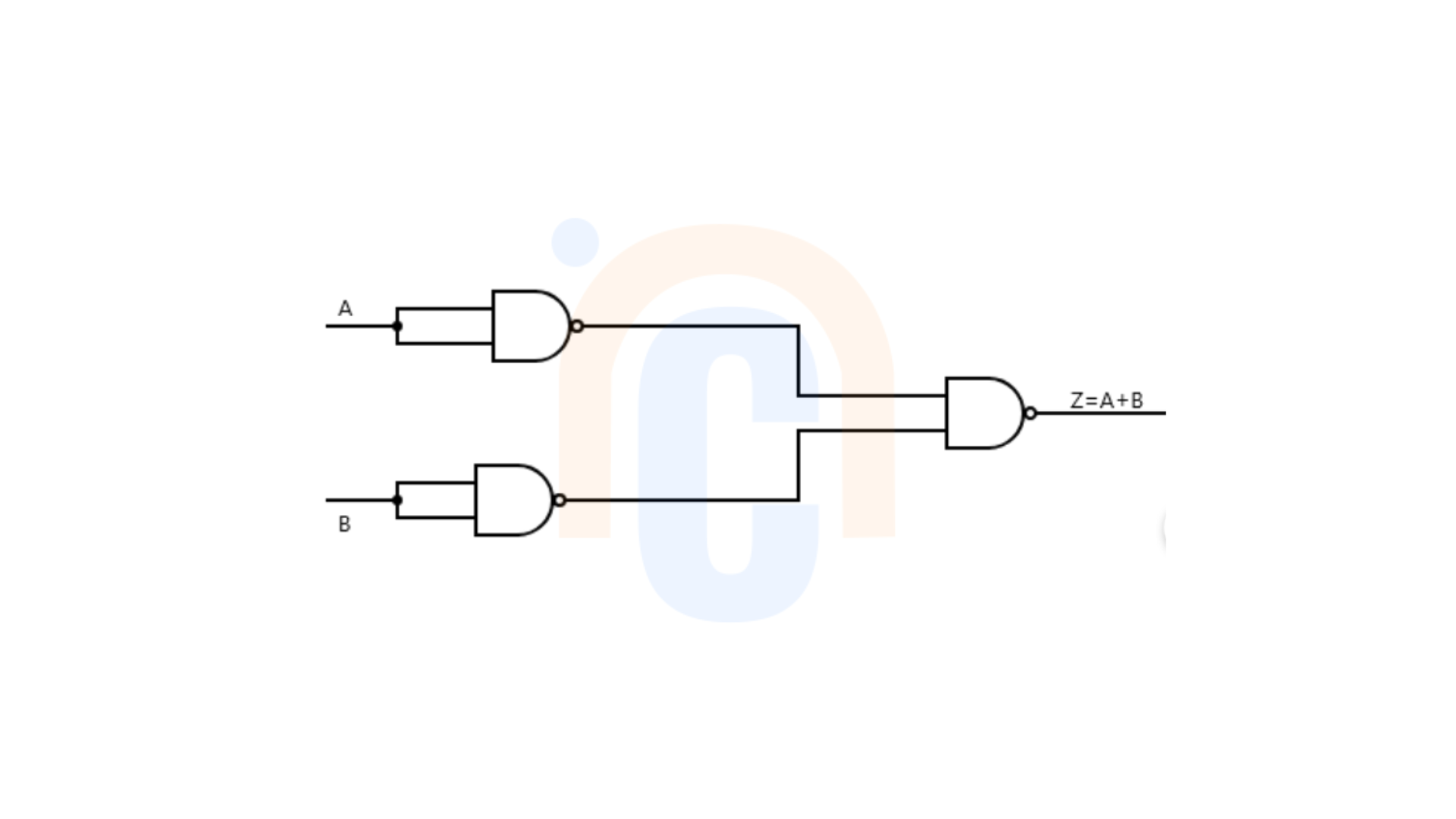
To obtain OR gate from NAND gates, we feed input A into a NAND with the input joined together to obtain a NOT (A), we feed input B into another NAND gate NAND with the input joined together to obtain NOT (B).
Now, the outputs NOT (A) and NOT (B) are supplied to separate inputs of another NAND gate.
Hence, it becomes a NAND(NOT(A) NOT (B)) or NAND \((\overline{A} \overline{B})\) which is equal to the OR gate.
Boolean formula: Z =\( \overline{Y_1 \cdot Y_2} = \overline{\overline{A} \cdot \overline{B}} = \overline{A} + \overline{B} = A + B\)
| A | B | Y1 | Y2 | Z |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
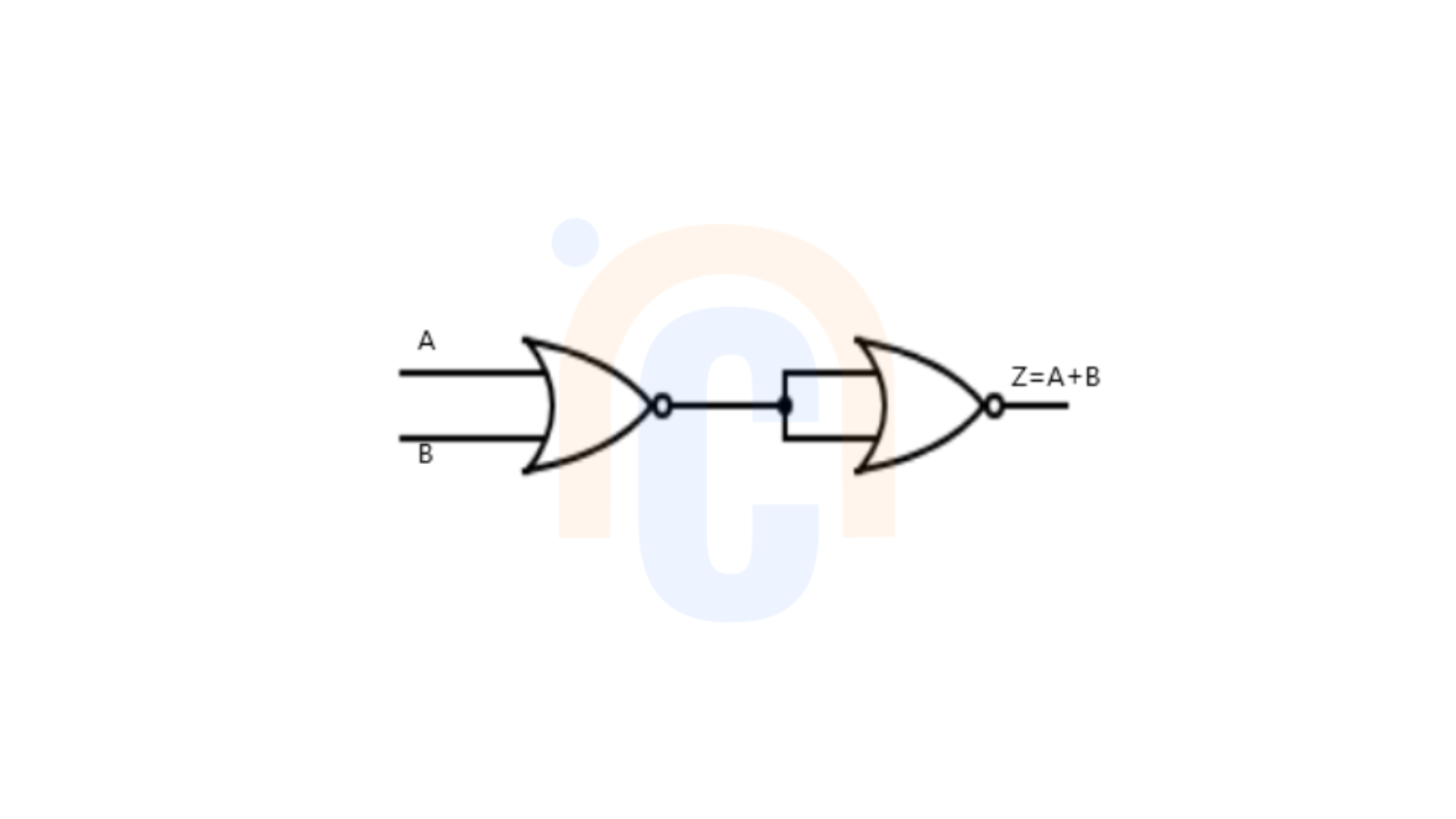
To obtain an OR gate from NOR gates, the input A and B is fed into a NOR gate (into the separate inputs), then the output say Y which is NOT(A or B) is input into two additional NOR gates, with the inputs combined to create a NOT (NOR Y), which functions as an OR gate.
Boolean formula: Z =\(\overline{Y}\) =\(\overline{\overline{A+B}
}\)=A+B
| A | B | Y | Z |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
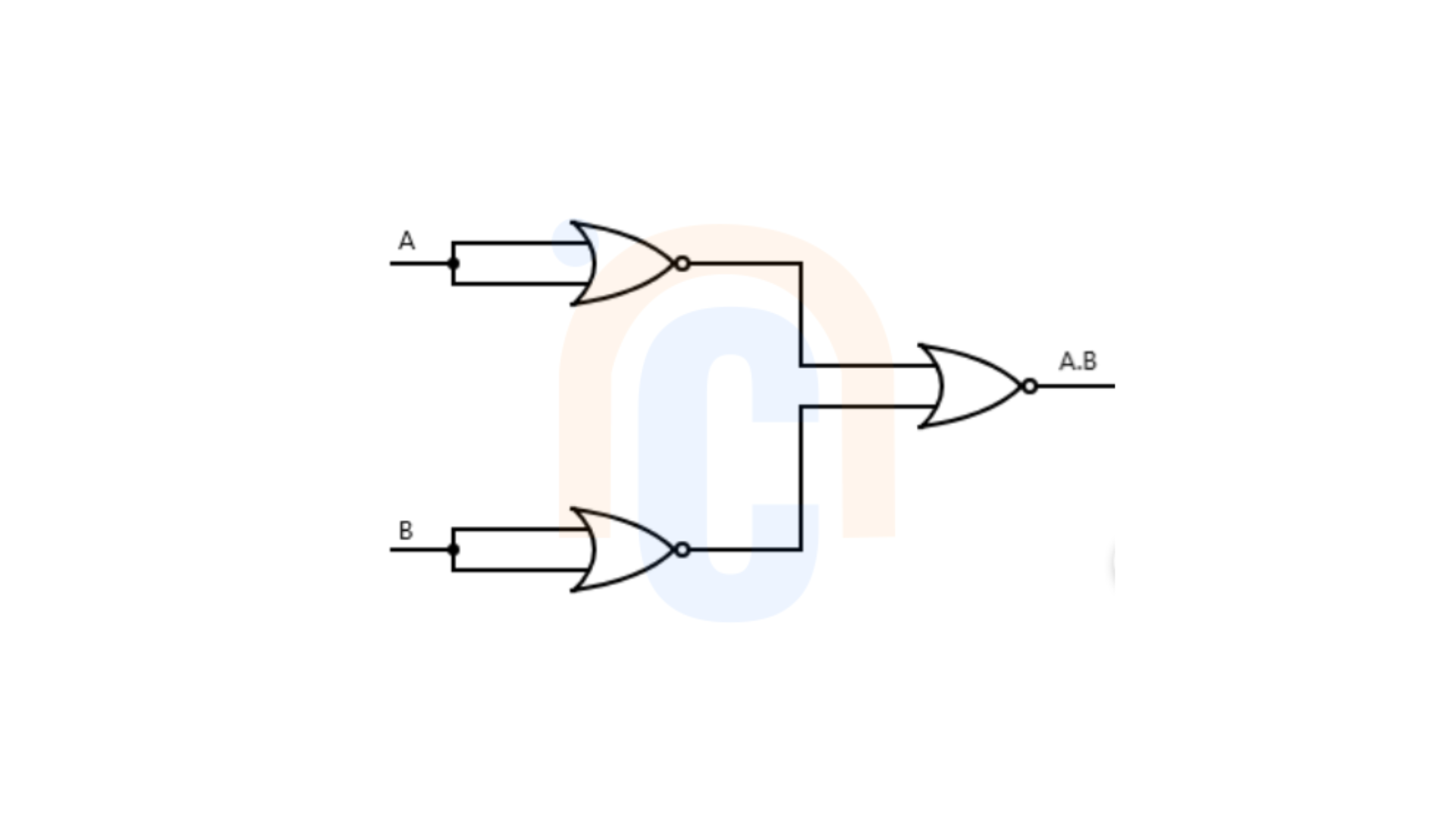
NOT(A or B) is input into two additional NOR gates, with the inputs combined to create a NOT (NOR Y), which functions as an OR gate.(i.e. NOT (A) to one Input terminal and NOT (B) to another terminal). The result will be an AND gate.
Boolean formula: Z=NOR\((\overline{AB})\) = \(\overline{\overline{A}+ \overline{B}}\) = \(\overline{\overline{A}}\).\(\overline{\overline{B}}\) = A.B
| A | B | \(\overline{A}\) | \(\overline{B}\) | Z |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
Note:
For clarity, joining the inputs of NAND and NOR gate gives us NOT gate because AND and OR act necessarily on two inputs. Hence, when the inputs NAND (or NOR) are joined to allow only one input, it opens the AND (or OR) circuit and acts as NOT circuit, since NAND actually means NOT-AND and NOR means NOT-OR. Thus, when the AND and NOR gates are eliminated, it transforms into a NOT gate.
