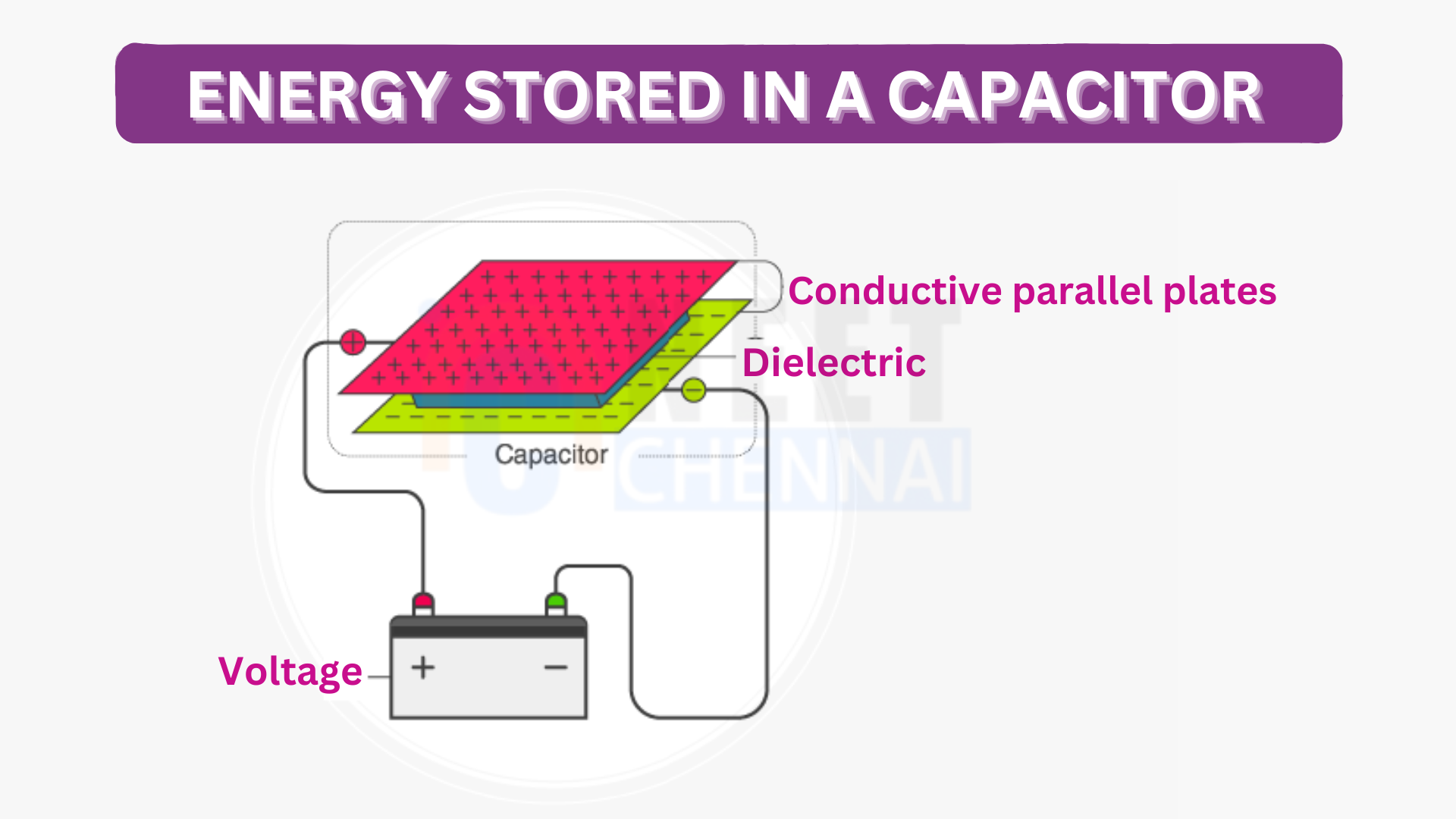
Derive the expression for energy stored in a charged capacitor.
Hint: The relationship between capacitance, charge, and electric potential is key here. The energy stored in a capacitor is equal to the work done in accumulating charge within it. This involves the relationship between electric potential and work.
Formula Used:
The relationship between voltage (\(V\)), charge (\(Q\)), and capacitance (\(C\)) is given by:
\(V = \frac{Q}{C}\)
where:
\(V\) is the electric potential,
\(C\) is the capacitance, and
\(Q\) is the charge on the capacitor.
The work done (\(dW\)) to move a small charge \(dQ\) into a capacitor at potential \(V\) is:
\(dW = V \, dQ\)
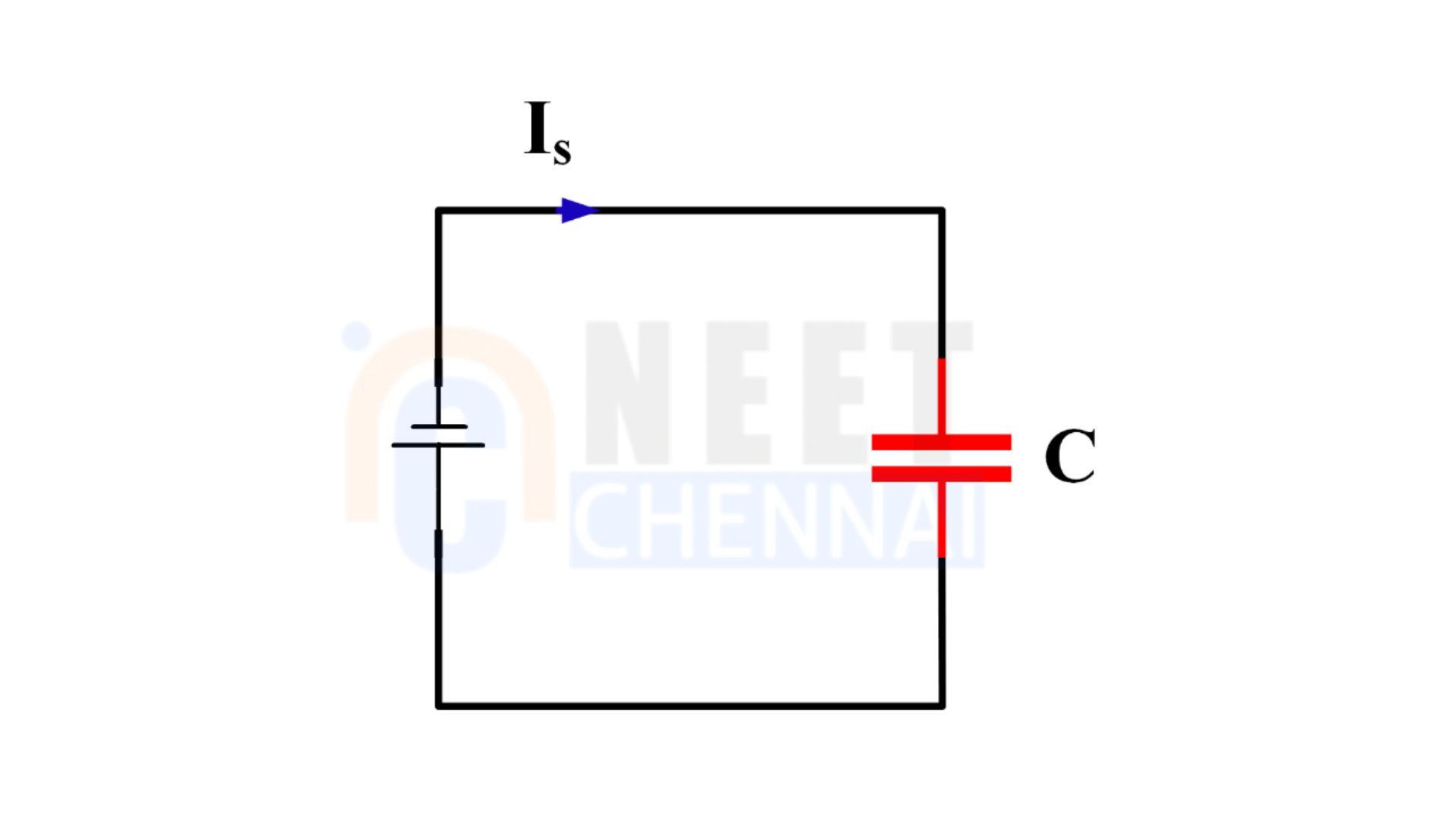
Solution:
Consider a capacitor in a circuit with voltage \(V\). The capacitance \(C\) and stored charge \( Q \) relate as:
\(Q = C \cdot V\)
Our aim is to find the energy stored in the capacitor.
According to electrostatic principles, the energy stored in a capacitor is equal to the work required to transfer the charge into the capacitor under potential \(V\). Thus:
\(dW = V \, dQ\)
Substitute \(V = \frac{Q}{C}\):
\(dW = \frac{Q}{C} \, dQ\)
To find the total work \(W\) done in moving the charge \(Q\) to the capacitor, integrate:
\(W = \int_0^Q \frac{Q}{C} \, dQ\)
\(W = \frac{1}{C} \int_0^Q Q \, dQ\)
Solving the integral:
\(W = \frac{1}{2} \frac{Q^2}{C}\)
Thus, the energy \(U\) stored in the capacitor is:
\(U = \frac{1}{2} \frac{Q^2}{C}\)
Using \(Q = C \cdot V\), we can also express this as:
\(U = \frac{1}{2} C V^2\)
Additional Information:
A capacitor is a device that stores energy by separating equal and opposite charges with a certain distance between them. The standard capacitors shown in textbooks are often parallel-plate capacitors. Capacitors are measured in farads (F), where one farad stores one coulomb (C) of charge across one volt (V) of potential difference.
Note: For a parallel-plate capacitor, capacitance \(C\) can also be calculated with the formula:
\(C = \frac{\varepsilon A}{d}\)
where \(\varepsilon\) is the permittivity of the medium between the plates, \(A\) is the plate area, and \(d\) is the distance between the plates. Substituting this expression for \(C\) allows us to express energy in terms of the area and separation of the plates.