(a)Draw logic diagram of EX-OR and EX-NOR gate using NAND gate and proof it using Boolean equation and truth table.
(b)Draw a logic diagram of EX-OR and EX-NOR gate using NOR gate and proof it using Boolean equation and truth table.
Hint:An Exclusive-OR (EX-OR) gate is a digital logic gate that produces a high output (true) when the number of high inputs is odd. Conversely, an Exclusive-NOR (EX-NOR) gate, which is essentially an EX-OR gate followed by a NOT gate, generates a high output (true) only when the number of high inputs is even. In simpler terms, the EX-NOR gate provides the complementary output of the EX-OR gate for identical input conditions.
Complete answer:
(a)
The logic diagram of EX-OR gate using NAND gate only is given as:
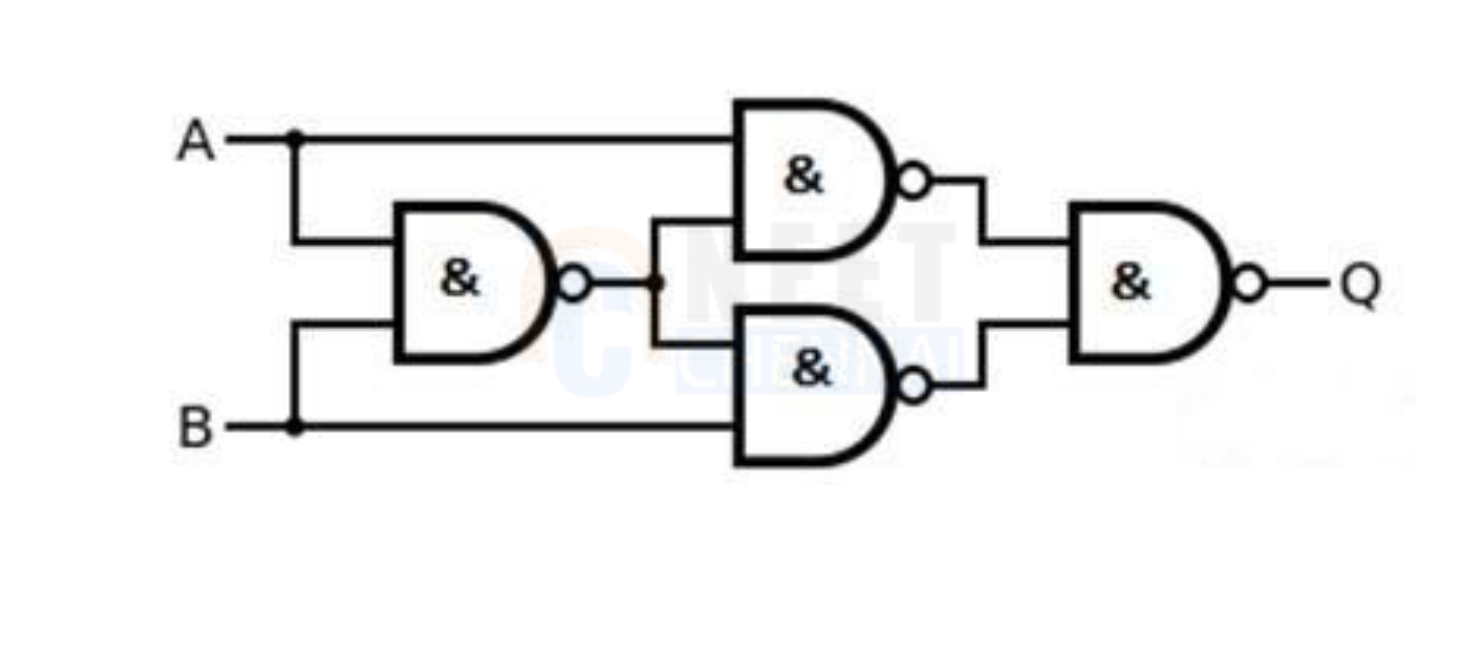To prove it using the Boolean equation, we know Exclusive-OR gate is “ A or B but not BOTH”.
Let us prove the above expression.
In the first case consider,
A = 0 and B = 0
∴A⊕B=0⊕0=0.\(\overline{0}\)+\(\overline{0}\).0=0.1+1.0=0
In the second case consider,
A = 0 and B= 1
∴A⊕B=0⊕1=0.\(\overline{1}\)+\(\overline{0}\).1=0.0+1.1=1
In third case consider,
∴A⊕B=1⊕0=1.\(\overline{0}\)+\(\overline{1}\).0=1.1+0.0=1
In fourth case consider,
A = 1 and B = 1
∴A⊕B=1⊕1=1.\(\overline{1}\)+\(\overline{1}\).1=1.0+0.1=0
So, it is proved that the Boolean expression for A ⊕ B is
Proof using truth table:
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Thus, it is proved using the Truth Table that EX-OR gate gives true output when the number of inputs is odd.
The logic diagram of EX-NOR gate using NAND gate is given as:
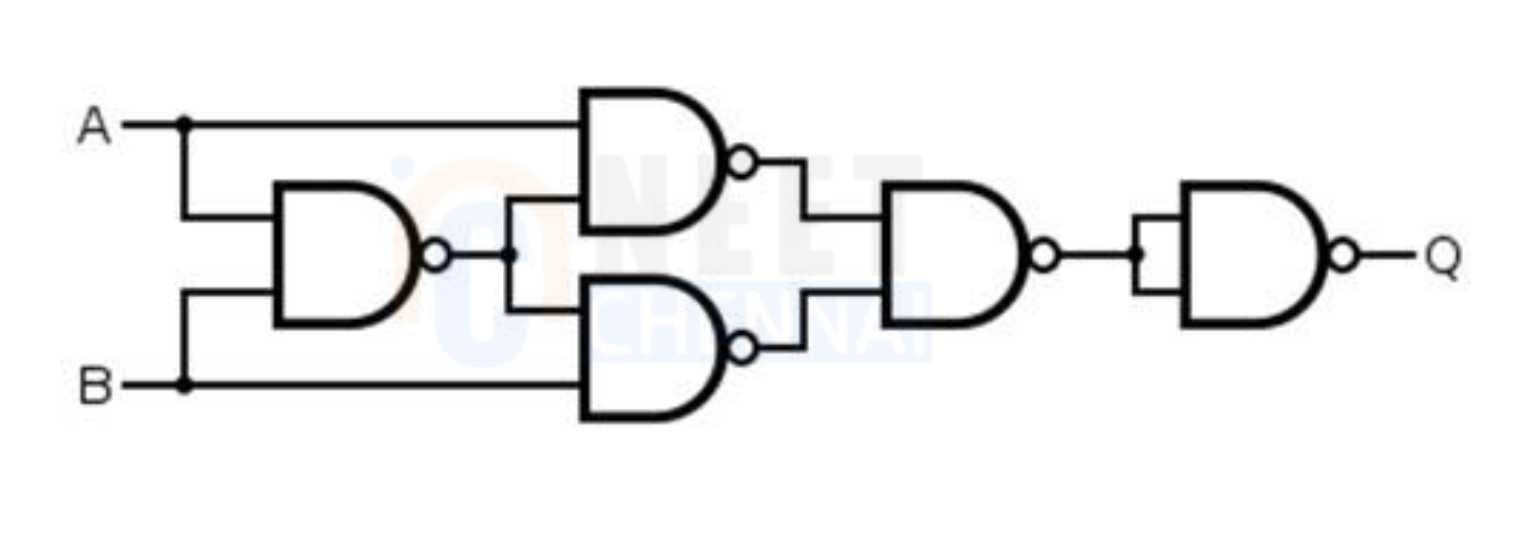To prove it using the Boolean equation, we know the Exclusive-NOR gate is represented as:
A ⊙ BConsider the following cases:
In the first case consider,
A = 0 and B = 0
∴ A ⊙ B = AB + ĀB̄ = (0 · 0) + (1 · 1) = 0 + 1 = 1
In the second case consider,
A = 0 and B = 1
∴ A ⊙ B = AB + ĀB̄ = (0 · 1) + (1 · 0) = 0 + 0 = 0
In third case consider,
A = 1 and B = 0
∴ A ⊙ B = AB + ĀB̄ = (1 · 0) + (0 · 1) = 0 + 0 = 0
In fourth case consider,
A = 1 and B = 1
∴ A ⊙ B = AB + ĀB̄ = (1 · 1) + (0 · 0) = 1 + 0 = 1
Thus, the Exclusive-NOR gate satisfies the Boolean equation A ⊙ B.
Proof using truth table:
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Thus, it is proved using the Truth Table that EX-NOR gate gives true output when the number of inputs is even.
(b)
The logic diagram of EX-OR gate using NOR gate only is given as:
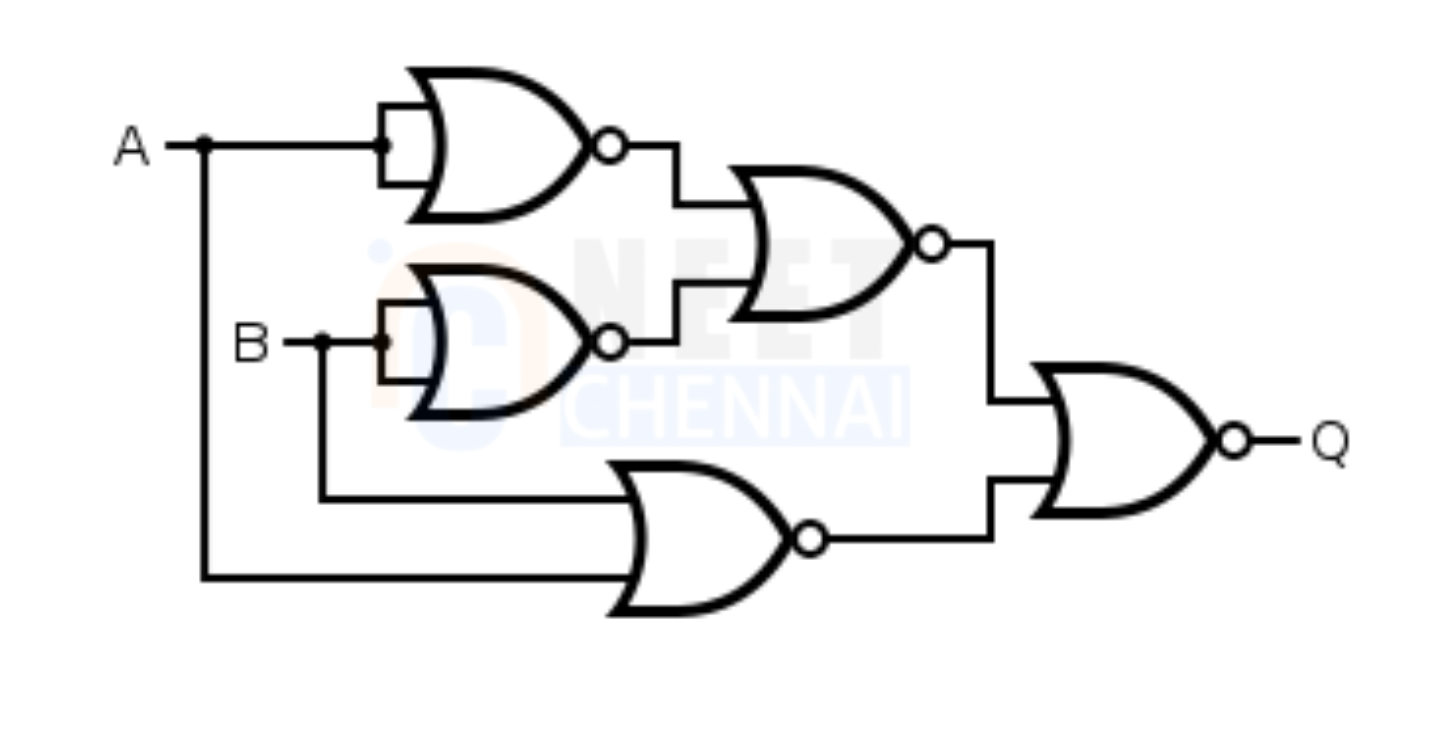To prove it using the Boolean equation, we know Exclusive-OR gate is “ A or B but not BOTH”.
Let us prove the above expression.
In the first case consider,
A = 0 and B = 0
∴A⊕B=0⊕0=0.1+1.0 = 0
In the second case consider,
A =0 and B = 1,
∴A⊕B = 0⊕1 =0.0+1.1=1
In third case consider,
A =1 and B =0,
∴A⊕B=1⊕0=1.1+0.0=1
In fourth case consider,
A=1 and B=1,
∴A⊕B=1⊕1=1.0+0.1=0
So, it is proved that the Boolean expression for A ⊕ B is , as this Boolean expression satisfied all output states with respect to an XOR gate’s inputs conditions.
Proof using truth table:
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Thus, it is proved using the Truth Table that EX-OR gate gives true output when the number of inputs is odd.
The logic diagram of EX-NOR gate using NOR gate is given as:
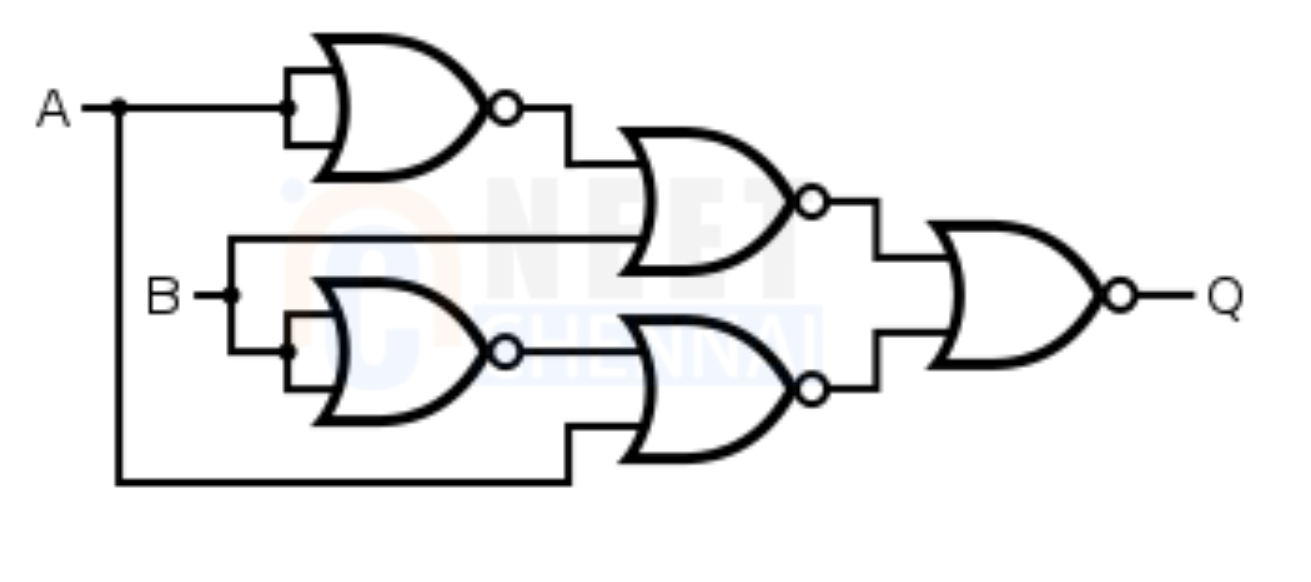To proof it using Boolean equation, we know Exclusive-NOR gate is “A⊙B”
In the first case consider,
In the second case consider,
A =o and B=1
∴A⊙B=AB+ĀB̄=0.1+1.0=0
In third case consider,
A=1 and B=0
∴A⊙B=AB+ĀB̄=1.0+0.1=0
In fourth case consider,
A=1 and B=1
∴A⊙B=AB+ĀB̄=1.1+0.0=1
Hence, it is proved that EX-NOR gate is A ⊙ B .
Proof using truth table:
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Thus, it is proved using the Truth Table that EX-NOR gate gives true output when the number of inputs is even.
Note:
All advanced logic gates can be derived using fundamental logic gates. Therefore, it is essential to have a clear understanding of the basic logic gates and their operations. Referring to their truth tables and Boolean expressions can be highly beneficial in resolving any challenges encountered during the process of building complex logic gates from basic ones.
