Derive mirror equation. State any three experimental observations of photoelectric emission.
Hint: In a spherical mirror, the distance of the object from the mirror’s pole is represented by \(u\) (object distance), the distance of the image by \(v\) (image distance), and the focal length by \(f\), which is the distance between the pole and the principal focus. The relationship between these quantities is given by the mirror equation:
\(\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\)
This equation applies universally to all spherical mirrors, regardless of the position of the object.
Step-by-Step Derivation of the Mirror Formula
To derive this formula, consider two similar right-angled triangles, \(\triangle A’B’F\) and \(\triangle MPF\), as shown below:
Similar Triangles:
Since \(\triangle A’B’F\) is similar to \(\triangle MPF\),
\(\frac{B’A’}{PM}=\frac{B’F}{FP}\)
Since \(PM = AB \), we can write:
\(\frac{B’A’}{BA}=\frac{B’F}{FP}\tag{1}\)
Relation between Image and Object Distance:
Given that \(\angle APB = \angle A’PB\) , we also have:
\(\frac{B’A’}{BA} = \frac{B’P}{BP} \tag{2}\)
Using Equations (1) and (2):
Equating these ratios, we obtain:
\(\frac{B’F}{FP} = \frac{B’P – FP}{FP} = \frac{B’P}{BP}\)
Using the values \(B’P = -v \), \(FP = -f\), and \(BP = -u\), we arrive at:
\(\frac{1}{v} + \frac{1}{u} = \frac{1}{f}\) This is the mirror equation, which relates the object distance, image distance, and focal length for any spherical mirror.
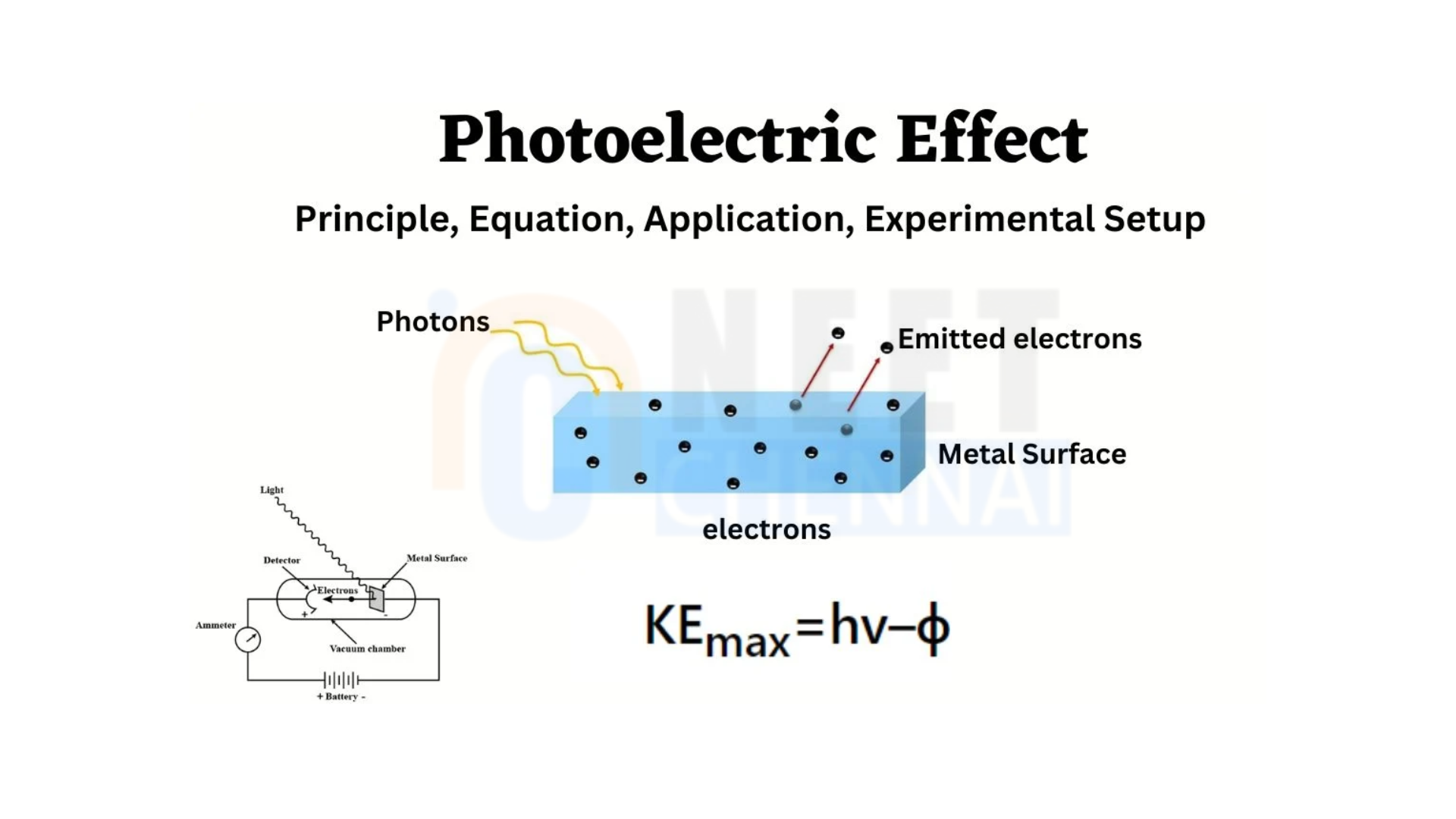
Observations of Photoelectric Emission
Threshold Frequency: Photoelectric emission only occurs if the frequency \(nu\) of the incident light exceeds a certain threshold frequency \(nu_0\) specific to the material, as only photons above this frequency have sufficient energy to release electrons.
Instantaneous Emission: Emission of electrons begins almost instantaneously upon exposure to light, implying that no delay exists between the arrival of photons and the ejection of electrons, which supports the particle nature of light.
Dependence on Light Intensity: The number of photo-electrons emitted is directly proportional to the intensity of the light, but the kinetic energy of the emitted electrons depends only on the light’s frequency, not its intensity, as per Einstein’s photoelectric equation:
\(K_{\text{max}} = h\nu – \phi\)
where \(K_{\text{max}}\) is the maximum kinetic energy of the emitted electrons, \(h\) is Planck’s constant, \(nu\) is the frequency of the incident light, and \(phi\) is the work function of the material.
Note: The mirror equation is universally applicable to all spherical mirrors for any object position.