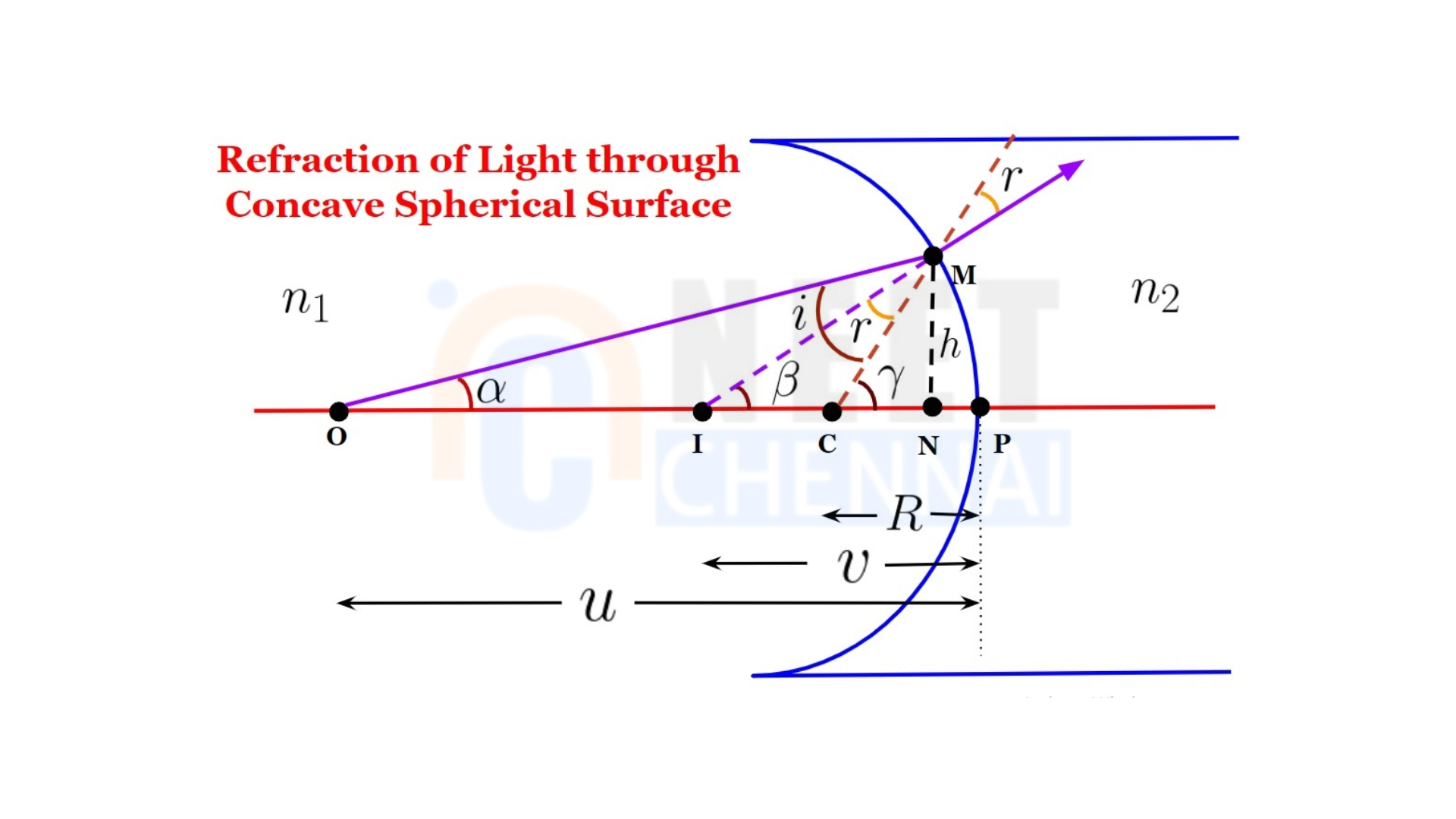
Derive the following expression for the refraction at concave spherical surface:

\(\frac{μ}{v}−\frac{1}{u}=\frac{μ−1}{R}\)

Hint:A spherical mirror is a section of a sphere with a reflective surface. If the inner surface is reflective, the mirror is concave; if the outer surface reflects, it is convex. In this case, we are working with a concave mirror and need to derive the related expression.

Solution:

Consider a concave mirror, represented by \(MPN\), with \(mu\) as the refractive index of the medium surrounding the mirror. Here:

– \(P\) is the mirror’s pole,

– \(O\) is the center of curvature, and

– \(PC\) is the principal axis of the spherical mirror.

We place a point object at \(O\). One incident ray travels along \(C\) and remains perpendicular to the surface, thus continuing straight through \(PX\). Another incident ray, \(OA\), refracts at point \(A\) and bends toward the normal. These two rays intersect at point \(I\), forming a virtual image.

Let the angles these rays make with the principal axis be \(\alpha\), \(\beta\), and \(\gamma\) respectively.

By Snell’s Law, the refractive index is:

\(\mu = \frac{\sin i}{\sin r}\)

where \(i\) is the angle of incidence and \(r\) the angle of refraction.

For small angles \(i\) and \(r\), we approximate:

\(\sin i \approx i \quad \text{and} \quad \sin r \approx r\)

so that:

\(\mu = \frac{i}{r}\)

leading to:

\(i = \mu r\)

Using the Exterior Angle Theoremin \(\triangle AOC\):

\(\gamma = i + \alpha \Rightarrow i = \gamma – \alpha\)

Similarly, in \(\triangle IAC\):

\(\gamma = \beta + r \Rightarrow r = \gamma – \beta\)

Substitute \(i\) and \(r\)from these into Snell’s Law:

\(\gamma – \alpha = \mu (\gamma – \beta)\)

Since for a spherical surface, \(\text{angle} = \frac{\text{arc}}{\text{radius}}\), we can write:

\(\alpha = \frac{PA}{OP}, \quad \beta = \frac{PA}{IP}, \quad \gamma = \frac{PA}{CP}\)

Substitute these expressions:

\(\frac{PA}{PC} – \frac{PA}{PO} = \mu \left( \frac{PA}{PC} – \frac{PA}{PI} \right)\)

Simplifying by canceling \( PA \) from both sides:

\(\frac{1}{PC} – \frac{1}{PO} = \mu \left( \frac{1}{PC} – \frac{1}{PI} \right)\)

Applying the sign convention:

– \(PC = -R\) (radius of curvature),

– \(PI = -v\) (image distance),

– \(PO = -u\) (object distance),

we substitute to get:

\(\frac{1}{-R} – \frac{1}{-u} = \mu \left( \frac{1}{-R} – \frac{1}{v} \right)\)

Expanding and rearranging:

\(\frac{\mu – 1}{R} = \frac{\mu}{v} – \frac{1}{u}\)

This gives us the desired expression for a concave mirror.

Note on Cartesian Sign Convention:

• Distances measured from the mirror’s pole.
• Positive distances are measured in the direction of incident light, while negative distances are measured opposite to it.
• Heights measured upward from the principal axis are positive, and those downward are negative.