Derive an Expression for Electric Potential (NEET Physics)

Derive an expression for electric potential at point due to an electric dipole.
Discuss the special cases.

Hint: An electric dipole consists of two charges that are equal in magnitude (q) but opposite in polarity. (i.e. one is a positive charge and other is a negative charge). The two charges are separated by a distance of 2a.
Formula used: V

$={\displaystyle \frac{Kq}{r}}$ ${(1\pm x)}^n\approx 1\pm n\mathrm{x,}$

if x is very much small.

Complete step by step answer:
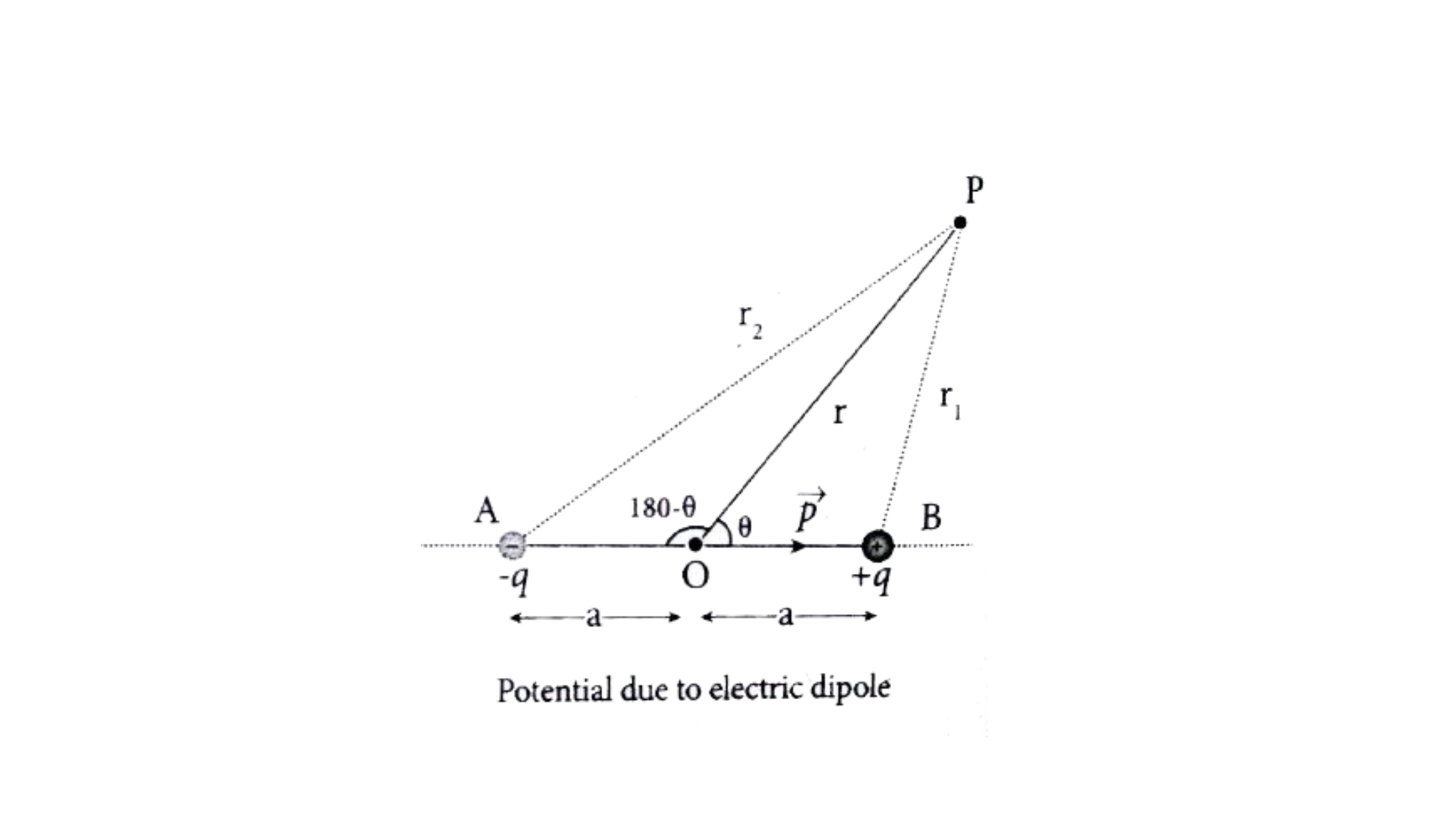
An electric dipole consists of a pair of charges that have the same magnitude \((q)\) but are opposite in nature. (i.e. one is a positive charge and other is a negative charge). The two charges are spaced apart by a distance of \(2a\). An electric dipole is characterized by a property known as the dipole moment, represented as \(P = 2qa\). Below is an illustration of an electric dipole.

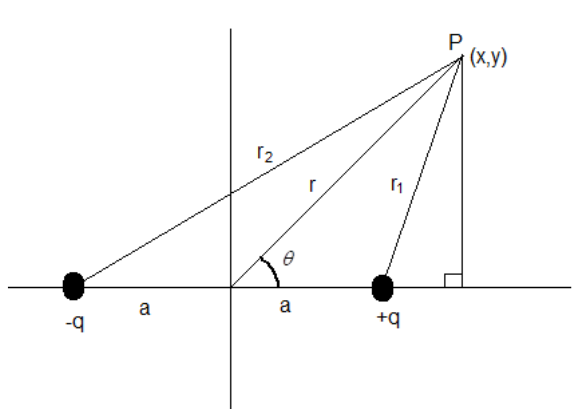
Let an electric dipole with charges +q and –q lie on x-axis with the origin as the midpoint of the dipole.
Consider a point P at the coordinates (x,y). The distance of the point from origin be r making an angle θ with positive x-axis.

Electric potential due to a charge q at a point, which is at a distance r from the charge is given as 

$V={\displaystyle \frac{Kq}{r}}$

Where V is the potential due to the charge and K is permittivity of free space. Now, the electric potential at point P will be due two charges (+q and -q).
Let the potential due to charge +q be

$V_{\mathrm{1,}}$

Let the potential due to charge -q be 

$V_{\mathrm{2,}}$

Let the total electric potential due to both the charges be V.
Since, electric potential is a scalar quantity, 

$V=V_1+V_2$

If you see the given figure,

$V_1={\displaystyle \frac{Kq}{r_1}}$………………(i).
Since, is right-angled triangle, 

${r_1}^2={(x-a)}^2+y^2$

$\Rightarrow r_1=\sqrt{{(x-a)}^2+y^2}$

Substitute the value of 

$r_1$

in equation (i).
Therefore, 

$V_1={\displaystyle \frac{Kq}{\sqrt{{(x-a)}^2+y^2}}}$ /And $V_2=-{\displaystyle \frac{Kq}{r_2}}$………. (ii).
Is also a right-angled triangle. Therefore, 

${r_2}^2={(x+a)}^2+y^2$ $\Rightarrow r_2=\sqrt{{(x+a)}^2+y^2}$

Substitute the value of $r_2$/in equation (ii).
Therefore, 

$V_2={\displaystyle \frac{-Kq}{\sqrt{{(x+a)}^2+y^2}}}$

This implies that 

$V=V_1+V_2={\displaystyle \frac{Kq}{\sqrt{{(x-a)}^2+y^2}}}-{\displaystyle \frac{Kq}{\sqrt{{(x+a)}^2+y^2}}}$

 

$V=Kq\left({\displaystyle \frac{1}{\sqrt{{(x-a)}^2+y^2}}}-{\displaystyle \frac{1}{\sqrt{{(x+a)}^2+y^2}}}\right)$…….(iii)
Consider the expression

$\sqrt{{(x\pm a)}^2+y^2}$

open up the brackets.

$\Rightarrow \sqrt{x^2\pm 2ax+a^2+y^2}$…………… (1)
But 

$x^2+y^2=r^2$

Therefore, expression (1) can be written as

$\sqrt{r^2\pm 2ax+a^2}$

Since r>>>>a, 

$\sqrt{r^2\pm 2ax+a^2}\approx \sqrt{r^2\pm 2ax}$

From the figure we know, 

$x=rcos\theta$

Substitute the value of x in the above equation.
Therefore,

$\sqrt{r^2\pm 2ax}=\sqrt{r^2\pm 2ar\cos \theta }$

Take 

$r^2$

as a common term.

$\Rightarrow \sqrt{r^2\pm 2ar\cos \theta }=r\sqrt{1\pm {\displaystyle \frac{2a\cos \theta }{r}}}$

…….(2).
Here, 

${\displaystyle \frac{2a\cos \theta }{r}}$

is a very much small value because r>>>>a.Any term 

${(1\pm x)}^n\approx 1\pm n\mathrm{x \; ,}$

if x is a very much small value or almost equal to zero.
Let us use the same concept in equation (2).
Therefore, 

$r\sqrt{1\pm {\displaystyle \frac{2a\cos \theta }{r}}}=r{\left(1\pm {\displaystyle \frac{2a\cos \theta }{r}}\right)}^{{\displaystyle \frac{1}{2}}}\approx r\left(1\pm {\displaystyle \frac{1}{2}}\left({\displaystyle \frac{2a\cos \theta }{r}}\right)\right)=r\left(1\pm {\displaystyle \frac{a\cos \theta }{r}}\right)=r\pm a\cos \theta$

Hence, we get that

$\sqrt{{(x\pm a)}^2+y^2}\approx r\pm a\cos \theta$

Therefore,

$\sqrt{{(x+a)}^2+y^2}\approx r+a\cos \theta$

and 

$\sqrt{{(x-a)}^2+y^2}\approx r-a\cos \theta$

Thence we can write equation (iii) as

$V=Kq\left({\displaystyle \frac{1}{r-a\cos \theta }}-{\displaystyle \frac{1}{r+a\cos \theta }}\right)$ $\Rightarrow V=Kq\left({\displaystyle \frac{r+a\cos \theta -\left(r-a\cos \theta \right)}{\left(r-a\cos \theta \right)\left(r+a\cos \theta \right)}}\right)$ $\Rightarrow V=Kq\left({\displaystyle \frac{r+a\cos \theta -r+a\cos \theta }{\left(r^2-a^2{\cos }^2\theta \right)}}\right)$ $$ $\Rightarrow V=Kq\left({\displaystyle \frac{2a\cos \theta }{\left(r^2-a^2{\cos }^2\theta \right)}}\right)$

We know that 2qa=P.

$\Rightarrow V={\displaystyle \frac{KP\cos \theta }{r^2-a^2{\cos }^2\theta }}$

……..(iv).
Therefore, the electric potential due to an electric dipole at a given point is equal to 

${\displaystyle \frac{KP\cos \theta }{r^2-a^2{\cos }^2\theta }}$

Special cases:
(i) When the given point is on the axial line of the dipole (i.e. 

$\theta =0$

).
Substitute

$\theta =0$

in equation (iv).
Therefore, 

$V={\displaystyle \frac{KP\cos 0}{r^2-a^2{\cos }^{2}0}}$

We know 

$\cos 0=1$

Hence, 

$V={\displaystyle \frac{KP\cos 0}{r^2-a^2{\cos }^{2}0}}={\displaystyle \frac{KP}{r^2-a^2}}$

(ii) When the given point is on the equatorial axis of the dipole (i.e. 

$\theta ={\displaystyle \frac{\pi }{2}}$

)
Substitute 

$\theta ={\displaystyle \frac{\pi }{2}}$

in equation (iv).
Therefore, 

$V={\displaystyle \frac{KP\cos \left({\displaystyle \frac{\pi }{2}}\right)}{r^2-a^2{\cos }^2\left({\displaystyle \frac{\pi }{2}}\right)}}$

We know 

$\cos \left({\displaystyle \frac{\pi }{2}}\right)=0$

Hence, 

$V={\displaystyle \frac{KP\cos \left({\displaystyle \frac{\pi }{2}}\right)}{r^2-a^2{\cos }^2\left({\displaystyle \frac{\pi }{2}}\right)}}={\displaystyle \frac{KP(0)}{r^2-a^2(0)}}=0$

When a point lies on the equatorial axis, the electric potential at that point becomes zero. You might question why

$r$

must be significantly larger than

$a$

.

Note:

This condition is justified because the concept of a dipole is essential in understanding molecules, which often exist as dipoles. For instance, in a water molecule, the bond between the oxygen and hydrogen atoms creates a dipole moment. The distance between these atoms is very small and can be considered negligible compared to the distance

$r$

from the midpoint of the dipole.