Key Concepts
Drift Velocity (\(v_d\)):
The average velocity that charged particles, such as electrons, acquire in a conductor when an electric field is applied.
Current (\(I\)):
The rate of flow of electric charge over time, given by:
\[
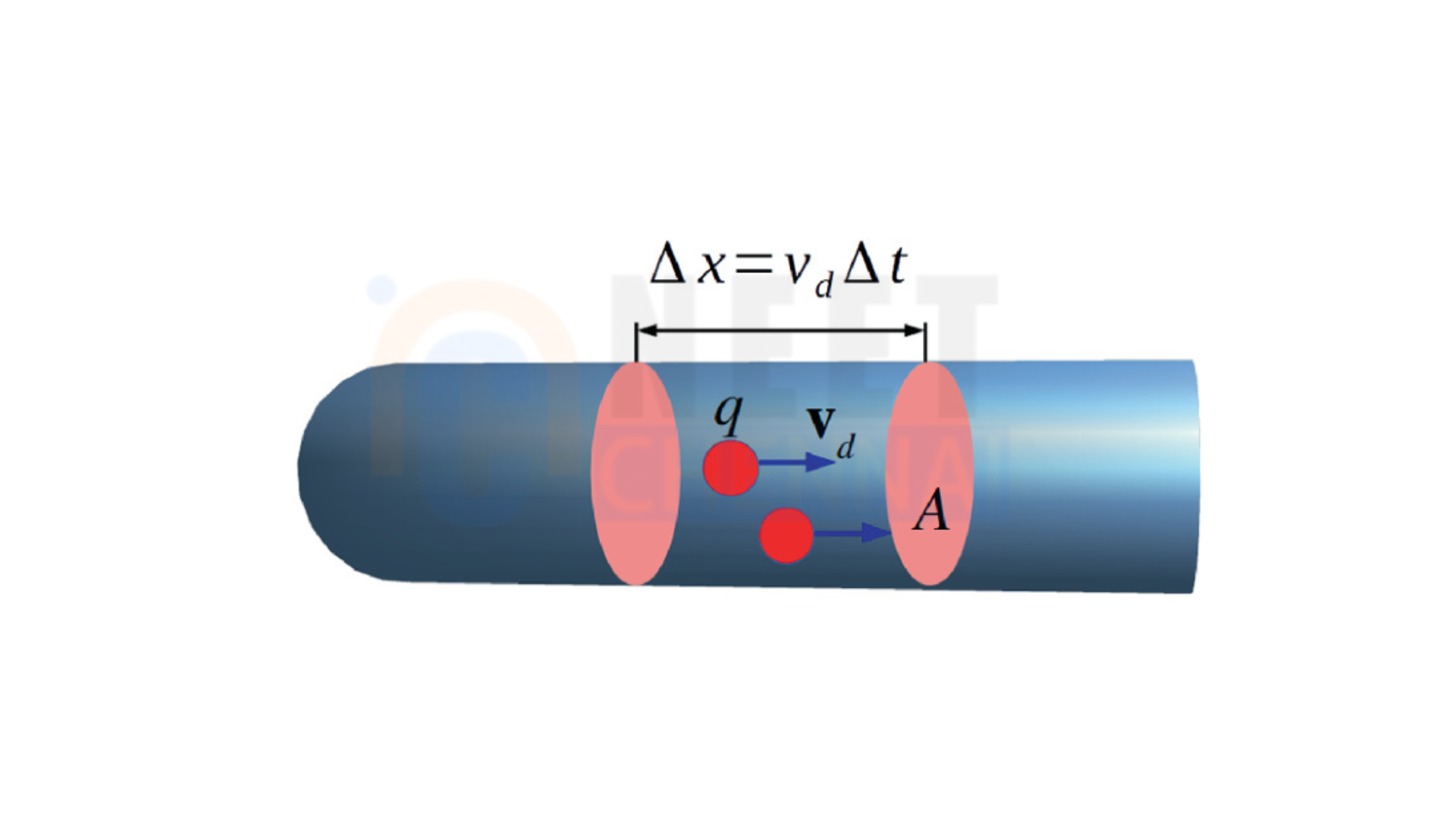
I = nqAv_d
\]
where:
– \( n \) = number density of charge carriers (electrons per unit volume),
– \( q \) = charge of an electron (approximately \(1.6 \times 10^{-19} \, C\)),
– \( A \) = cross-sectional area of the conductor,
– \( v_d \) = drift velocity.
Ohm’s Law:
This law relates current, voltage, and resistance in a conductor and is expressed as:
\[
V = IR
\]
Derivation Steps
Expressing Current in Terms of Drift Velocity:
From the current formula, we can rearrange it to find the drift velocity:
\[
v_d = \frac{I}{nqA}
\]
Using Ohm’s Law:
Ohm’s Law, which states \( V = IR \), can also be expressed using the electric field \( E \) and resistivity \( \rho \):
\[
I = \frac{V}{R}
\]
where the resistance \( R \) can be related to the resistivity by:
\[
R = \frac{\rho L}{A}
\]
where \( L \) is the length of the conductor. Substituting this into the equation gives:
\[
I = \frac{V A}{\rho L}
\]
Substitute Current into the Drift Velocity Equation:
Now, we can substitute \( I \) back into the drift velocity formula:
\[
v_d = \frac{V A}{\rho L n q A} = \frac{V}{\rho L n q}
\]
Relate Electric Field to Voltage:
The electric field \( E \) across a conductor of length \( L \) can be defined as:
\[
E = \frac{V}{L}
\]
Substituting this into the expression for drift velocity, we get:
\[
v_d = \frac{E L}{\rho L n q} = \frac{E}{\rho n q}
\]
Final Expression
The final equation for drift velocity of free electrons in a conductor is:
\(v_d = \frac{E}{\rho n q}\)
Notes
This expression shows that drift velocity depends on the electric field, the density of charge carriers, and the material’s resistivity. In practical applications, drift velocities are generally very low—typically only a few millimeters per second—due to frequent collisions of electrons with atoms within the conductor.