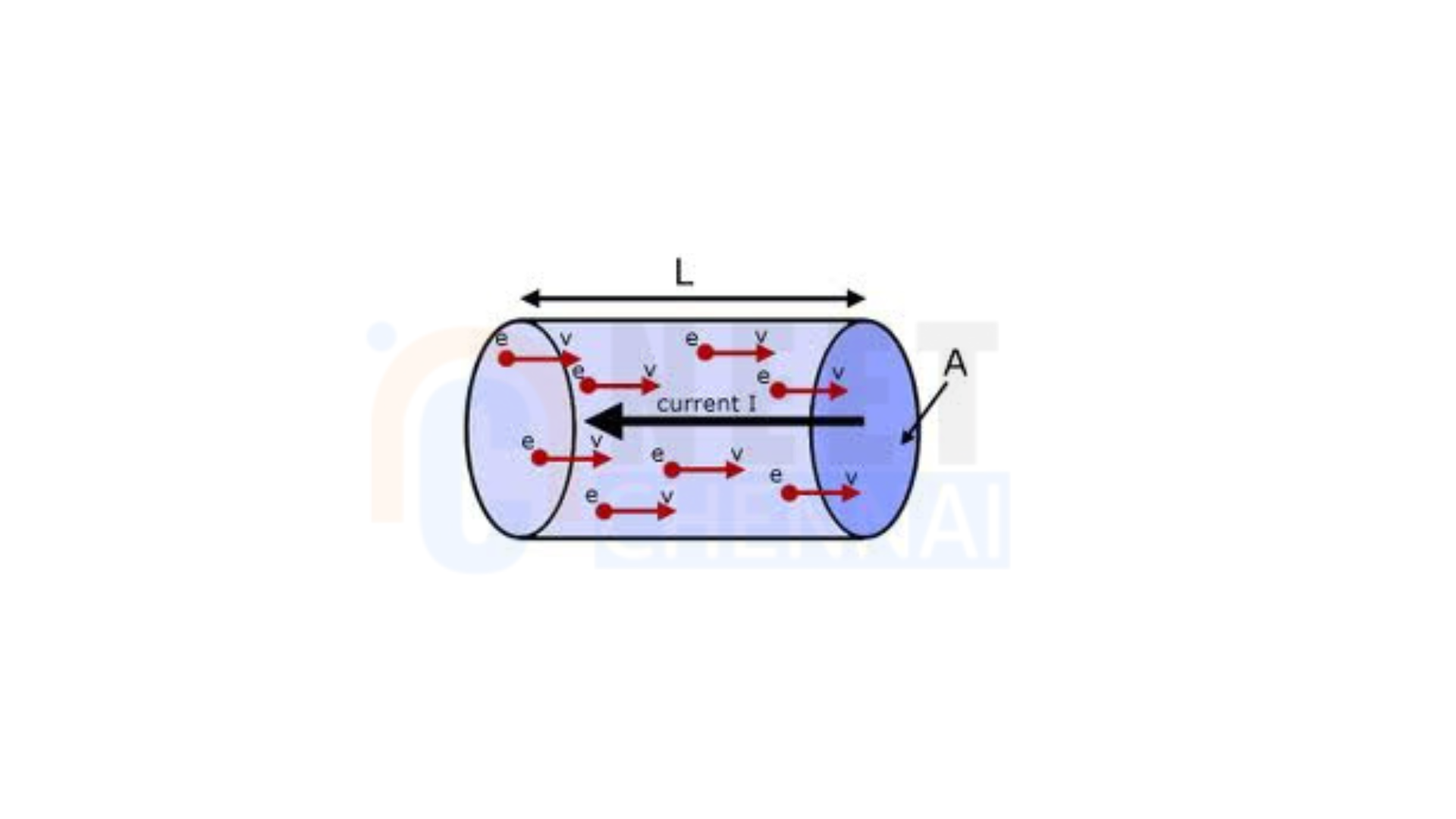
Derive an expression for drift velocity of free electrons in a conductor.
Hint: Think of electrons as extremely small free particles within a conductor that experience a force from an electric field. By calculating the force on each electron, we can determine its acceleration. The drift velocity refers to the average velocity of all the electrons in a specific region.
Relevant Formula:
The force acting on a charged particle within an electric field is described by:
\(F = qE ………..(1)\)where \( q \) represents the charge of the particle and \( E \) is the electric field strength.
The general kinematic equation is:
\(v = u + at …….(2)\)where \( v \) is the final velocity, \( u \)is the initial velocity, \( a \) is the acceleration, and \( t \) is the time duration.
Step-by-Step Solution:
Assume there’s an electric field \( E \) in the conductor. For this analysis, we will focus on a single electron and calculate its acceleration due to this electric field.
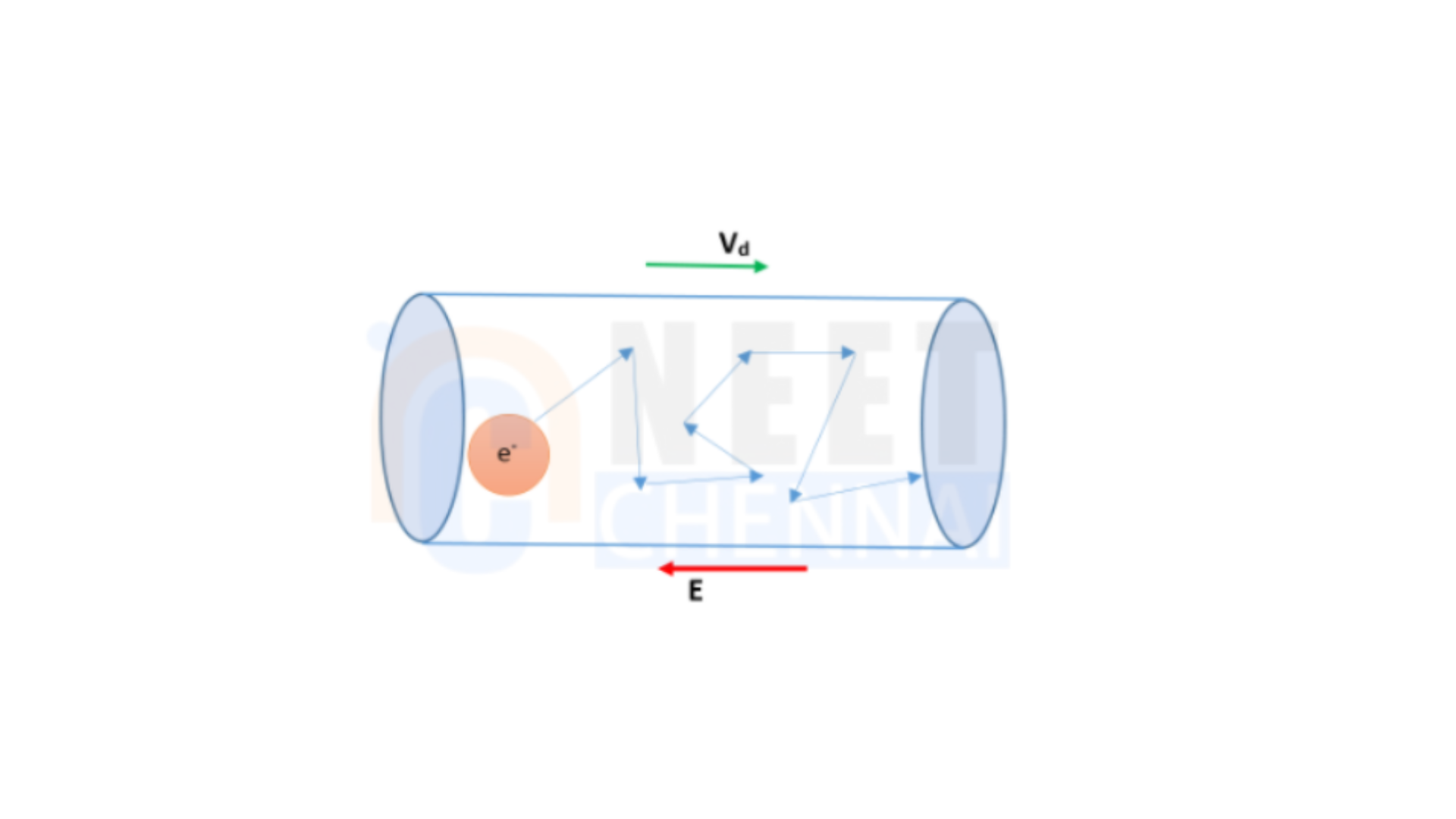
Since the force from the electric field is significantly greater than the forces arising from electron-electron interactions, we can neglect those interactions.
Let’s denote the charge of the electron as \(-e \).
Thus, the force acting on the electron is:
\( F = -eE \)To determine the electron’s acceleration, we apply Newton’s second law:
\( a = \frac{F}{m} = \frac{-eE}{m} \)where
represents the mass of the electron.
Next, we introduce the concept of relaxation time, which is the average time interval between two successive collisions of an electron in the conductor.
Let’s assume there are \( n \) electrons in the conductor at any moment.
The total relaxation time can be expressed as:
\( \tau = \tau_1 + \tau_2 + \tau_3 + \ldots + \tau_n \)where \(\tau_1, \tau_2, \tau_3, \ldots\) are the individual collision times for each electron.
The drift velocity is defined as the average velocity of all the electrons:
\( v_d = \frac{v_1 + v_2 + v_3 + \ldots + v_n}{n} \)Using the kinematic equation (2):
\(\frac{v_d = \left( u_1 + u_2 + \ldots + u_n \right) + a \left( \tau_1 + \tau_2 + \ldots + \tau_n \right)}{n}\)Assuming the initial average velocity is zero, we have:
\( v_d = 0 + a \left( \frac{\tau_1 + \tau_2 + \ldots + \tau_n}{n} \right) \)Thus, we can write:
\( v_d = a\tau \)Substituting for acceleration:
\( v_d = \left( \frac{-eE}{m} \right) \tau \)Therefore, the drift velocity can be expressed as:
\( v_d = \frac{-eE\tau}{m} \)Note: It’s important for students to understand this approach. Familiarity with the basic equations will allow you to easily derive this expression. It’s also worth noting that as the temperature of the conductor increases, atomic vibrations intensify, leading to a decrease in the time between collisions. This results in a reduced relaxation time, which means that drift velocity is inversely related to temperature: as temperature increases, drift velocity decreases.