State and explain Coulomb’s law in electrostatics.
Hint: When two or more charges are present, they exert forces on each other. Opposite charges attract, while like charges repel. This force is directly related to the magnitude of the charges and inversely related to the square of the distance between them.
Complete Answer:
Coulomb’s Law:
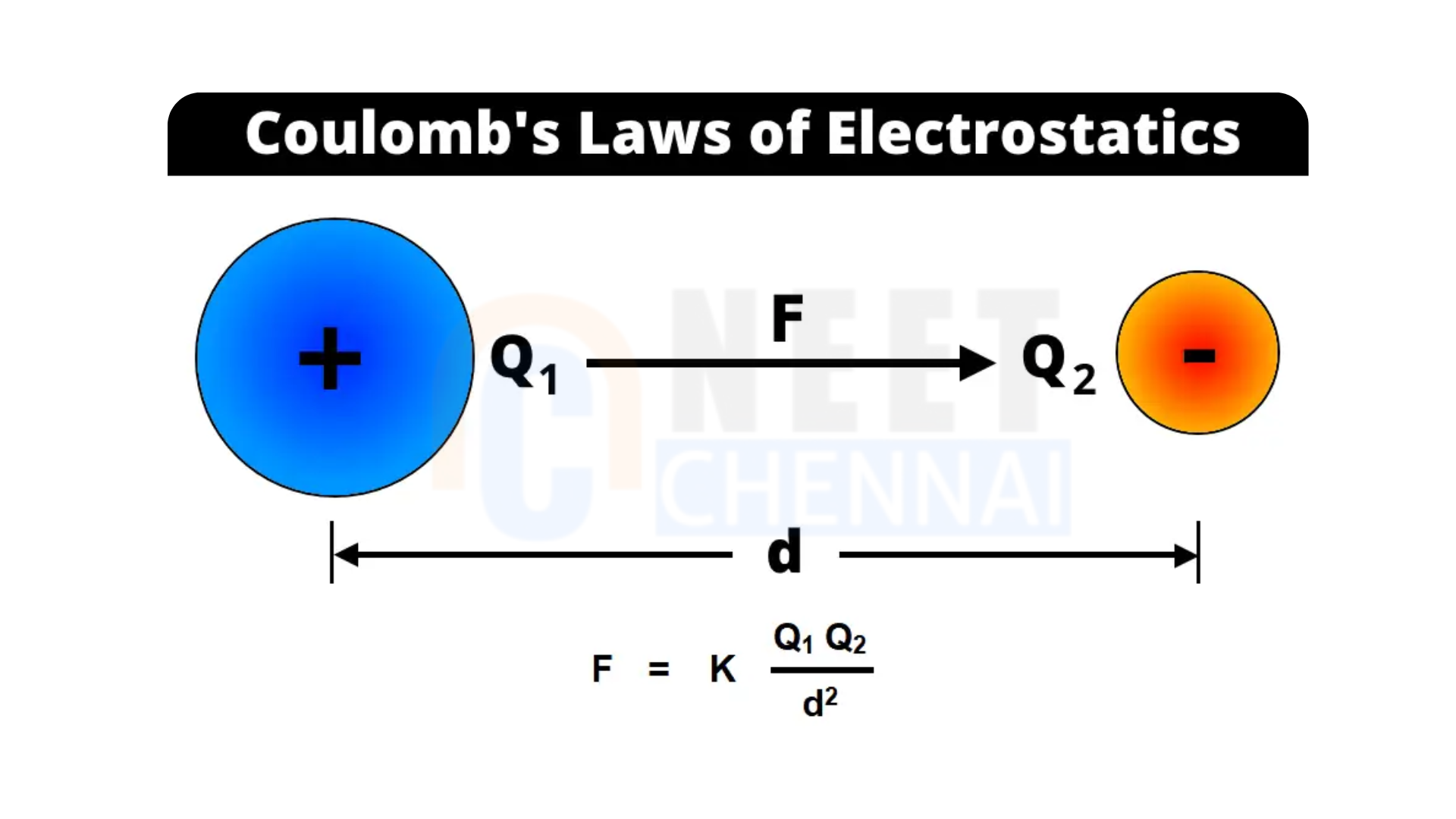
The electrostatic force between two stationary point charges is directly proportional to the product of their magnitudes and inversely proportional to the square of the distance between them. This force is directed along the line that joins the two charges.
Consider two point charges \(q_1\) and \(q_2\) separated by a distance \(r\). Let \( F \) be the electrostatic force between these charges. According to Coulomb’s law:
\(F \propto q_1 q_2 \quad \text{and} \quad F \propto \frac{1}{r^2}\)
Thus, the electrostatic force \(F\)can be expressed as:
\(F_e = K \frac{q_1 q_2}{r^2}\)
where:
– \(K\) is Coulomb’s constant, approximately \(9\)times \(10^9 \, \text{N} \cdot \text{m}^2/\text{C}^2\).
– \(r\) is the distance between the charges.
– \(K = \frac{1}{4 \pi \epsilon_0}\)and \(\epsilon_0\) is the permittivity of the medium.
Vector Form of Coulomb’s Law:
The force on \(q_1\) due to \(q_2\) is:
\(\vec{F}_{12} = K \frac{q_1 q_2}{r^2} \hat{r}_{21}\)
where \(\hat{r}_{21}\) is the unit vector from \(q_2\) to \(q_1 \). Similarly, the force on \(q_2\) due to \(q_1 \) is:
\(\vec{F}_{21} = K \frac{q_1 q_2}{r^2} \hat{r}_{12}\)
where \(\hat{r}_{12}\) is the unit vector from \(q_1\) to \(q_2\).
Position Vector Form of Coulomb’s Law:
Using position vectors \(\vec{r}_1\) and\(\vec{r}_2\) for \(q_1\) and \(q_2\) , the force \(\vec{F}_{12}\) can be expressed as:
\(\vec{F}_{12} = K \frac{q_1 q_2}{|\vec{r}_1 – \vec{r}_2|^3} (\vec{r}_1 – \vec{r}_2)\)
Note: Coulomb’s law is derived from empirical observations and is fundamental in nature. It describes a conservative force, meaning the work done in moving a charge in this field depends only on the initial and final positions.