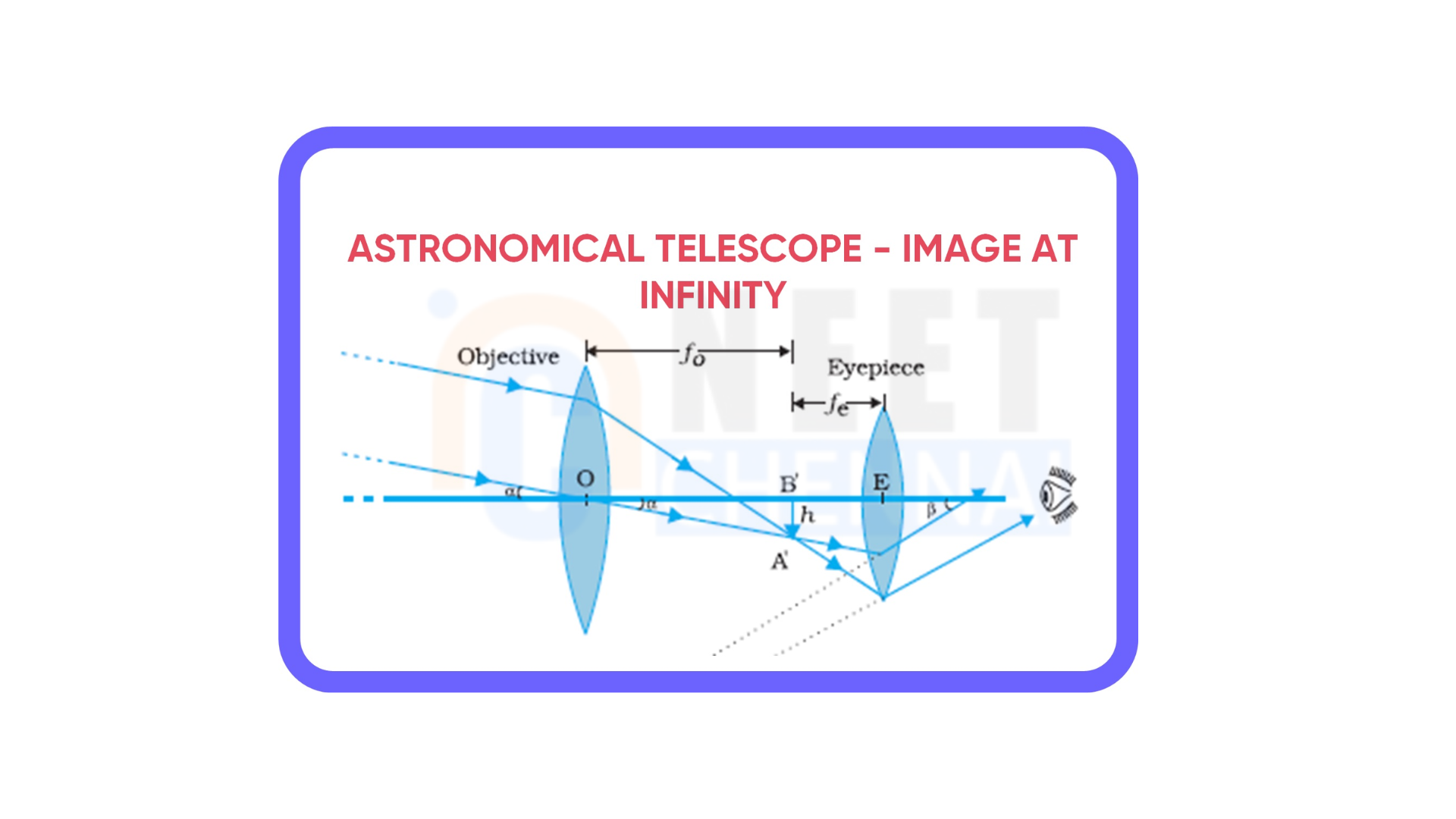
Describe the astronomical telescope on the basis of the following points:
(i) Labelled ray diagram.
(ii) Derivation of formula for magnifying power, when the final image is formed at the least distance of distinct vision.
(i) Labelled ray diagram.
(ii) Derivation of formula for magnifying power, when the final image is formed at the least distance of distinct vision.
An astronomical telescope is a device used to observe distant objects, particularly celestial bodies, by creating magnified images of them. It uses two key components: the objective lens and the eyepiece lens. The objective lens collects light and focuses it, and the light passes through the eyepiece lens, where it forms a magnified image.
Key Components and Functioning:
Objective Lens:
This lens, positioned at the end facing the distant object, has a larger aperture and focal length. It captures light from the distant object and focuses it into a real image.
Eyepiece Lens:
This smaller lens, through which the observer looks, has a smaller aperture and focal length. It magnifies the real image formed by the objective lens and creates a larger virtual image that the eye can perceive.
The two lenses are mounted in separate tubes. The eyepiece can slide inside the objective tube to adjust the distance between them for focusing.
When the telescope is aimed at a distant object, the objective lens forms a real image on its focal plane. The eyepiece then creates a magnified virtual image for the observer’s eye. In normal use, the final image is typically adjusted to form at infinity, reducing strain on the eye. However, if the eyepiece is adjusted closer to the first image, the image can be magnified further, with the maximum magnification achieved when the image is positioned at the near point.
Derivation of Magnification Formula:
Let \(f_0\)\(f_0\) and \(f_e\) be the focal lengths of the objective and eyepiece lenses, respectively. Assume the object is at a very large distance, \(u_0\), from the objective.
Angle Subtended by the Object:
The angle \(\alpha\) subtended by the object on the objective lens is given by:
\(| \alpha | \approx \tan(\alpha) = \frac{P’Q’}{f_0}\)
where \(P’Q’\) is the size of the first image formed by the objective lens.
Angle Subtended by the Image at the Eyepiece:
The eyepiece lens then magnifies this image, and the angle \(\beta\) subtended by the final image at the eyepiece is:
\(| \beta | \approx \tan(\beta) = \frac{P’Q’}{f_e}\)
Magnification:
The magnification or angular magnification \(m\) of the telescope is the ratio of the angle \(\beta\) (final image) to the angle \(\alpha\) (object):
\(m = \frac{\beta}{\alpha} = \frac{f_0}{f_e}\) This is the magnifying power when the final image is formed at infinity (normal adjustment).
Magnification at the Near Point:
If the telescope is adjusted to form the final image at the near point of the eye (distance \(D\)), the magnification increases. Using the lens equation for the eyepiece, where \(u = E’P’\) and \(v = -E’P’ = -D\), the equation becomes:
\(\frac{1}{v} – \frac{1}{u} = \frac{1}{f_e}\)
Simplifying, we get:
\(\frac{1}{E’P’} = \frac{1}{f_e} + \frac{1}{D} = \frac{f_e + D}{f_eD}\)
Therefore, the magnification for the near point is:
\(m = \frac{\beta}{\alpha} = -\frac{f_0}{f_e} \left(1 + \frac{f_e}{D}\right)\)
Notes:
- To achieve higher magnification, the focal length of the objective lens should be as long as possible, while the focal length of the eyepiece should be kept short.
- When the telescope is in normal adjustment, the final image is formed at infinity, causing the least strain on the eyes.
- Both lenses used in an astronomical telescope should be converging lenses.
- The image formed by the telescope is always inverted with respect to the object being observed. However, this inversion does not matter much when observing celestial bodies, which are typically spherical.