# 7 Powerful Area Formulas of Triangle You Must Know for NEET Success! 🚀
Triangles are everywhere! From the shape of a pizza slice to the pyramids of Egypt, they play a crucial role in geometry. But when it comes to exams like NEET, you need to go beyond just recognizing triangles—you must master the area formulas of a triangle to ace your test!
In this article, I’ll break down different ways to calculate a triangle’s area, share real-life applications, and give you some pro tips to remember these formulas forever! Let’s dive in.
Key Highlights
- Learn 7 area formulas of a triangle (Basic to Advanced)
- Master the NEET exam formulas quickly
- Understand real-life applications of these formulas
- Bonus tips and tricks for easy memorization
1. The Basic Formula (Half-Base-Height Formula)

The most commonly used formula to find the area of a triangle is:
🌟 Area = (1/2) × Base × Height
For example, if you have a triangle with a base of 10 cm and a height of 5 cm, the area is:
📈 (1/2) × 10 × 5 = 25 cm²
✅ Pro Tip: If the height is not given, use trigonometry to find it!
2. Heron’s Formula (For When You Know All Three Sides)

What if you don’t know the height of the triangle? That’s where Heron’s Formula saves the day!
🌟 Area = √[s(s-a)(s-b)(s-c)]
Where s is the semi-perimeter:
📈 s = (a + b + c) / 2
Example: A triangle with sides 7 cm, 8 cm, and 9 cm:
📈 s = (7+8+9) / 2 = 12 📈 Area = √[12(12-7)(12-8)(12-9)] = 26.83 cm²
✅ Pro Tip: This formula is useful for irregular triangles in NEET problems!
3. Area Using Trigonometry (For Non-Right Angled Triangles)

If you have two sides and an included angle (θ), use: 🌟 Area = (1/2) × a × b × sin(θ)
Example: If two sides are 6 cm and 8 cm, with an included angle of 60°: 📈 (1/2) × 6 × 8 × sin(60) = 20.8 cm²
✅ Pro Tip: Remember sin 30° = 1/2, sin 45° = √2/2, sin 60° = √3/2 to quickly solve these in exams!
4. Equilateral Triangle Formula

For an equilateral triangle (all sides equal), use: 🌟 Area = (√3/4) × a²
Example: Side = 6 cm 📈 Area = (√3/4) × 6² = 15.58 cm²
✅ Pro Tip: This formula is direct and helps save time in competitive exams!
5. Isosceles Triangle Formula
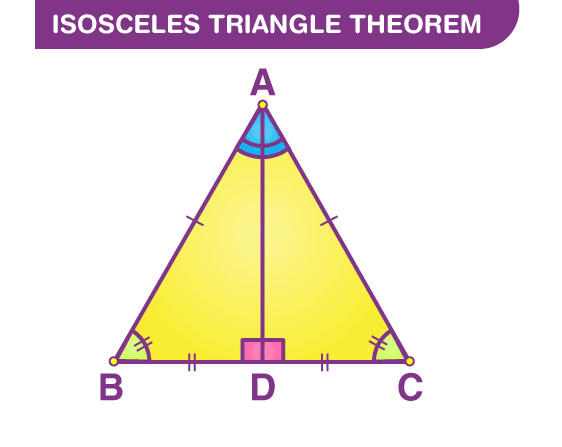
For an isosceles triangle (two equal sides), the formula is: 🌟 Area = (b/4) × √(4a² – b²)
Where b = base, and a = equal side.
Example: If a = 5 cm, b = 6 cm: 📈 Area = (6/4) × √(4(5²) – 6²) = 12 cm²
6. Right-Angled Triangle Formula
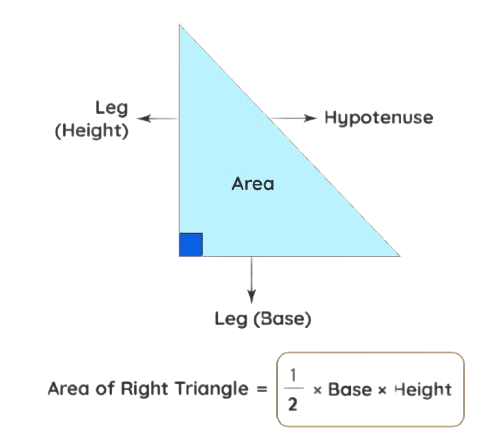
For a right-angled triangle, the basic formula applies:
🌟 Area = (1/2) × Base × Height
✅ Pro Tip: If the hypotenuse is given, use Pythagoras’ Theorem to find the missing side!
7. Using Coordinate Geometry
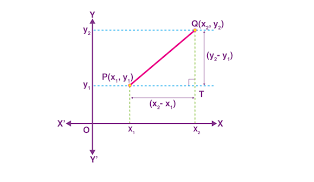
If you have a triangle with vertices
, use: 🌟 Area = (1/2) × | x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂) |
✅ Pro Tip: This is used in graph-based NEET questions.
How These Formulas Help in NEET?
- Direct Questions: Expect at least one question from triangle area formulas.
- Conceptual Questions: Problems combining trigonometry & coordinate geometry.
- Application-Based Questions: Real-life applications in physics & engineering.
Final Thoughts
Mastering the area formulas of a triangle is a game-changer for NEET aspirants. If you can recognize which formula to use in different cases, you’ll save time and score higher.
🛠️ Quick Recap:
- Basic formula → Use base & height.
- Heron’s formula → Use when all three sides are given.
- Trigonometry formula → Use for angles.
- Special cases → Equilateral, isosceles, and right-angled triangles.
- Coordinate geometry → Use for graphs & maps.
So, which formula do you find the easiest? Let me know in the comments below! 🚀💪


