(a) Logic Diagrams and Proofs for EX-OR and EX-NOR Gates Using NAND Gates
EX-OR Gate: The logic diagram for an EX-OR gate constructed with NAND gates is shown below.
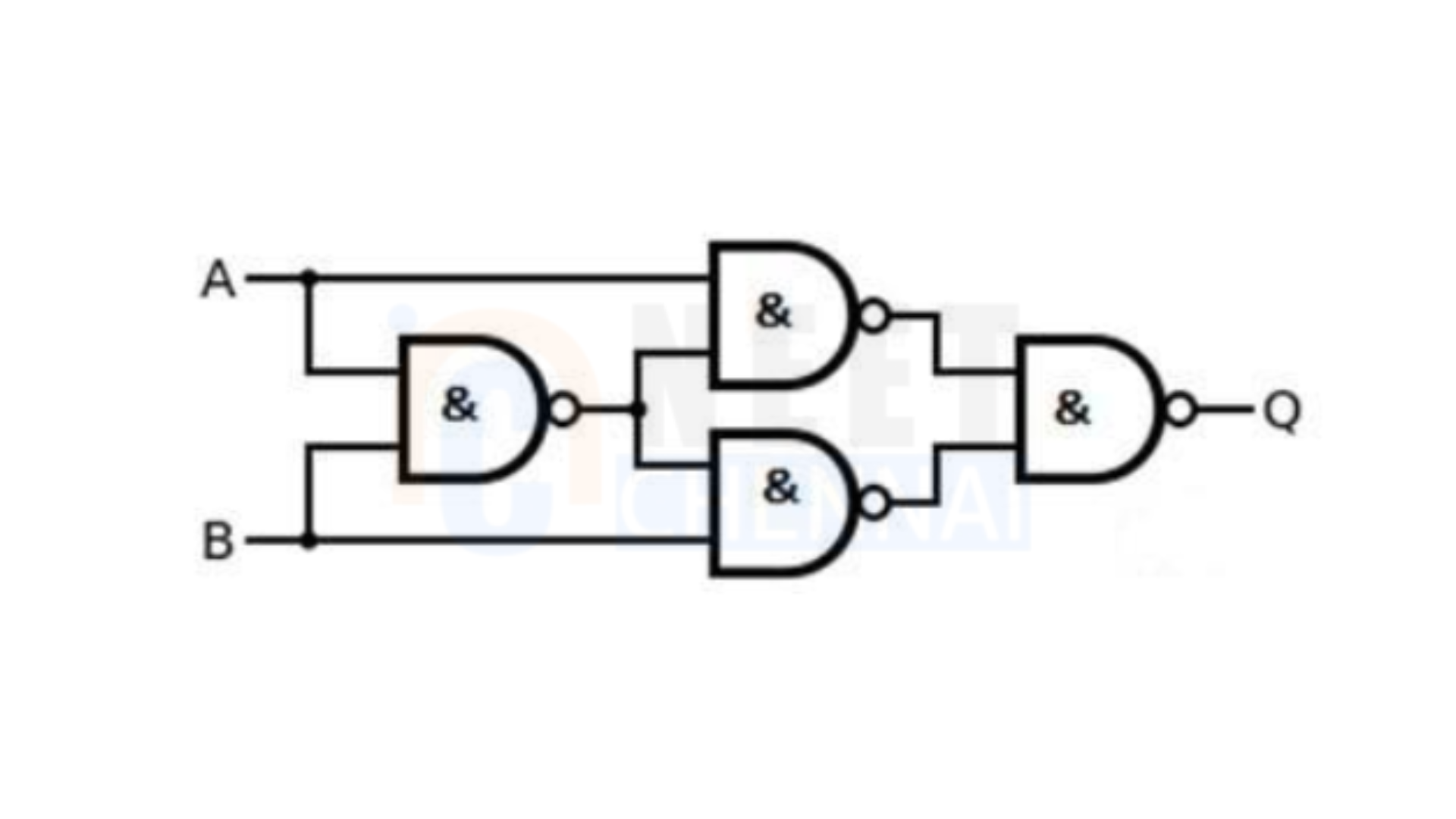
To prove the functionality using Boolean equations, the Exclusive-OR (EX-OR) gate can be defined as “A or B, but not both.” Let’s verify this:
Case 1:
A = 0, B = 0
∴ A ⊕ B = 0 ⊕ 0 = 0
Case 2:
A = 0, B = 1
∴ A ⊕ B = 0 ⊕ 1 = 1
Case 3:
A = 1, B = 0
∴ A ⊕ B = 1 ⊕ 0 = 1
Case 4:
A = 1, B = 1
∴ A ⊕ B = 1 ⊕ 1 = 0
Thus, the Boolean expression for A ⊕ B is \(AB’ + A’B\)confirmed by the above cases.
Truth Table for EX-OR:
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
This truth table confirms that the EX-OR gate outputs true when the number of inputs is odd.
EX-NOR Gate: The logic diagram for an EX-NOR gate using NAND gates is shown below.
To prove this with a Boolean expression, the Exclusive-NOR (EX-NOR) gate can be expressed as:
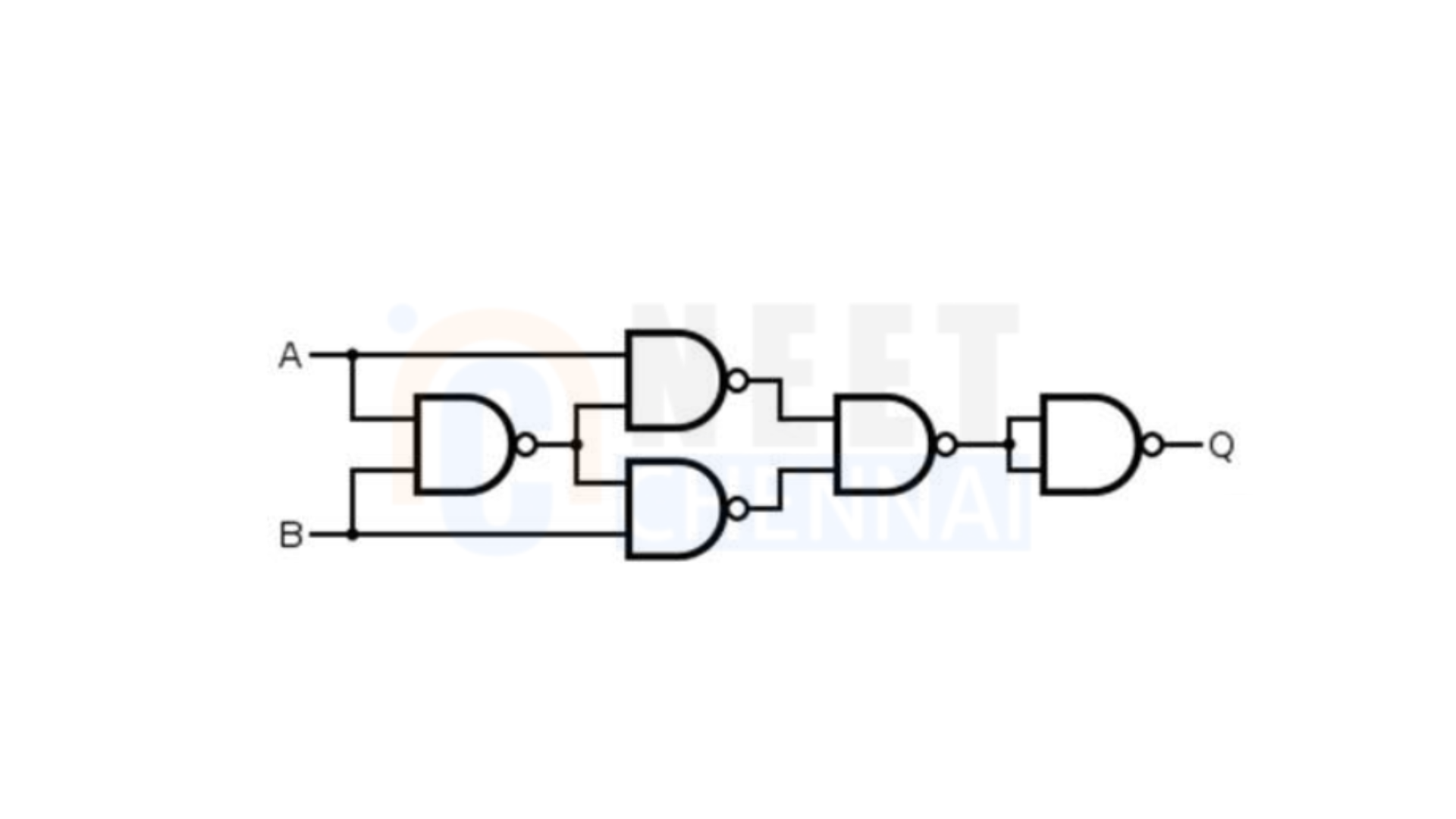
Case 1:
A = 0, B = 0
∴ \(A\odot B=1\)
Case 2:
A = 0, B = 1
∴ \(A\odot B=0\)
Case 3:
A = 1, B = 0
∴ \(A\odot B=0\)
Case 4:
A = 1, B = 1
∴ \(A\odot B=1\)
Thus, the expression for EX-NOR is \(AB+A’B’\).
Truth Table for EX-NOR:
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
This truth table shows that the EX-NOR gate outputs true when the number of inputs is even.
(b) Logic Diagrams and Proofs for EX-OR and EX-NOR Gates Using NOR Gates
EX-OR Gate: The logic diagram for an EX-OR gate constructed using NOR gates is illustrated below.
To validate the behaviour, we can again define the EX-OR gate as “A or B, but not both,” and check:
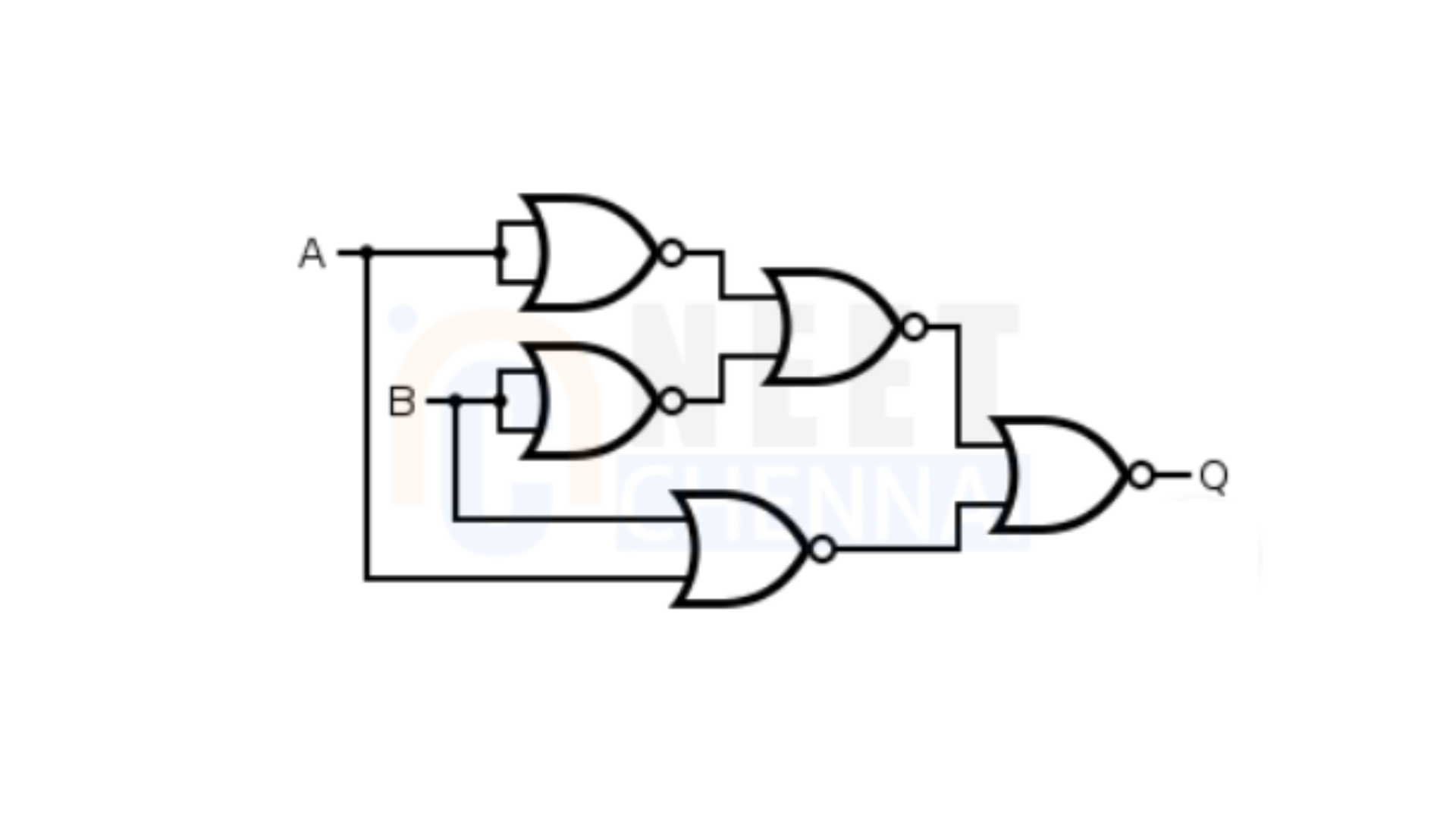
Case 1:
A = 0, B = 0
∴ A ⊕ B = 0
Case 2:
A = 0, B = 1
∴ A ⊕ B = 1
Case 3:
A = 1, B = 0
∴ A ⊕ B = 1
Case 4:
A = 1, B = 1
∴ A ⊕ B = 0
The expression for A ⊕ B remains \(AB’+A’B\)
Truth Table for EX-OR:
| Input A | Input B | Output Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
This confirms that the EX-OR gate produces a true output when the number of inputs is odd.
EX-NOR Gate: The logic diagram for an EX-NOR gate using NOR gates is also shown below.
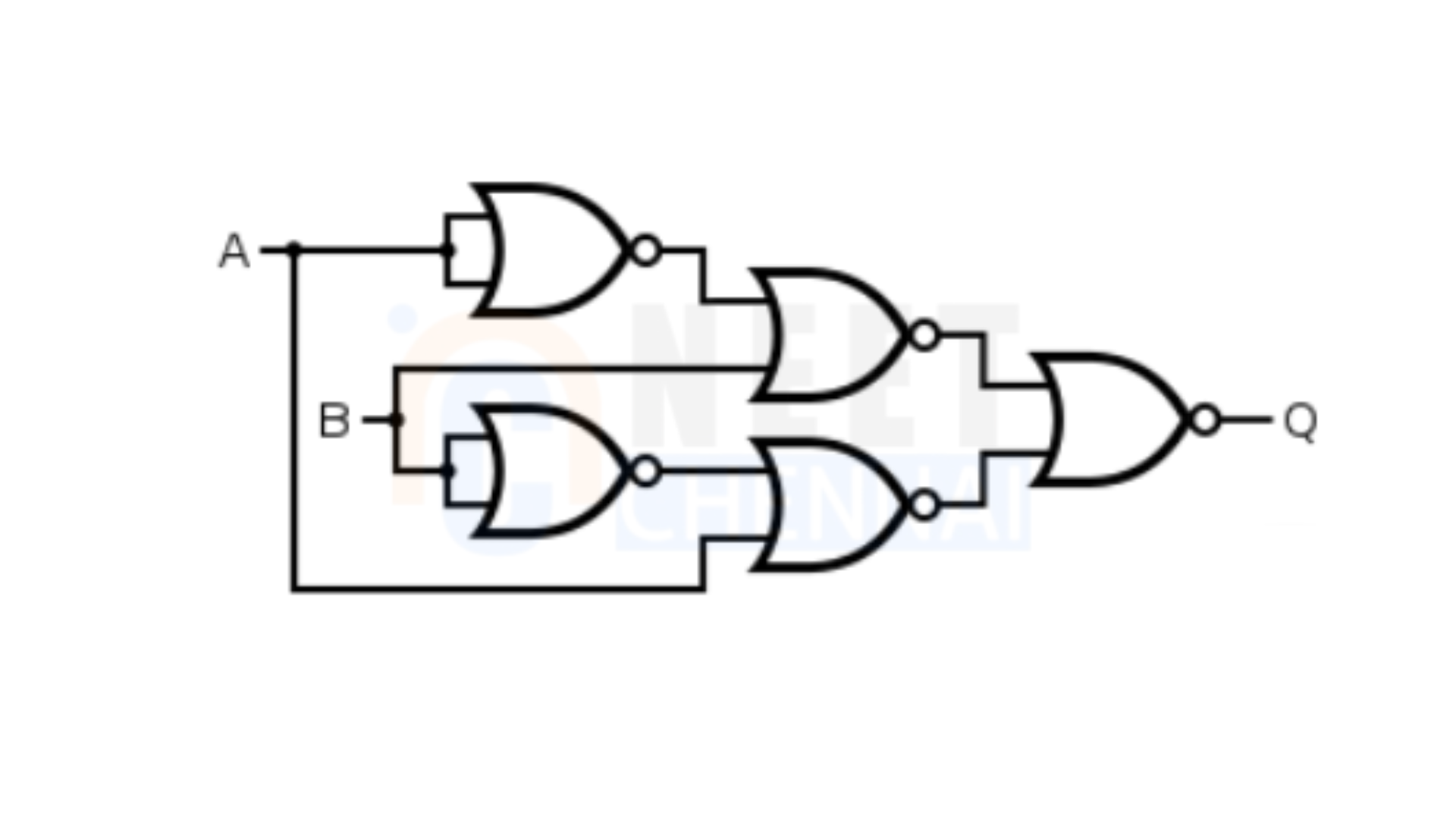
The proof follows similarly:
Case 1:
A = 0, B = 0
∴ \(A\odot B=1\)
Case 2:
A = 0, B = 1
∴ \(A\odot B=0\)
Case 3:
A = 1, B = 0
∴ \(A\odot B=0\)
Case 4:
A = 1, B = 1
∴\(A\odot B=1\)
The expression for EX-NOR is \(AB + A’B’\).
Truth Table for EX-NOR:
| Input A | Input B | Output Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
This table verifies that the EX-NOR gate yields a true output when the number of inputs is even.
Note: All complex logic gates can be constructed using basic gates. Understanding how to build these basic gates and referencing their truth tables and Boolean expressions can greatly aid in designing more complex logic circuits.