Define relaxation time of the free electrons drifting in a conductor: How is it related to the drift velocity of free electrons? Use this relation to deduce the expression for the electrical resistivity of the material.
Hint: Drift velocity is directly proportional to relaxation time. Write the equation for the current passing through the conductor. Replace the drift velocity with its expression in terms of relaxation time. Utilize the formula for the applied electric field and Ohm’s law to derive the expression for resistance in terms of length l and cross-sectional area A .
Formula used:
\(v_d = −\frac{eE}{m}τ\)\(I =−neAv_d\)
V = IR
Complete step by step answer:
Relaxation time is defined as the duration between two consecutive collisions of electrons in a conductor when an electric current is passing through it. It is denoted by τ.
Relation between drift velocity of the electrons \((v_d)\) and relaxation time (\tau) is given by,
\(v_d=−\frac{eE}{m}τ \)…(1)
Where, E: Electric field
M: mass of electron
E: charge of electron
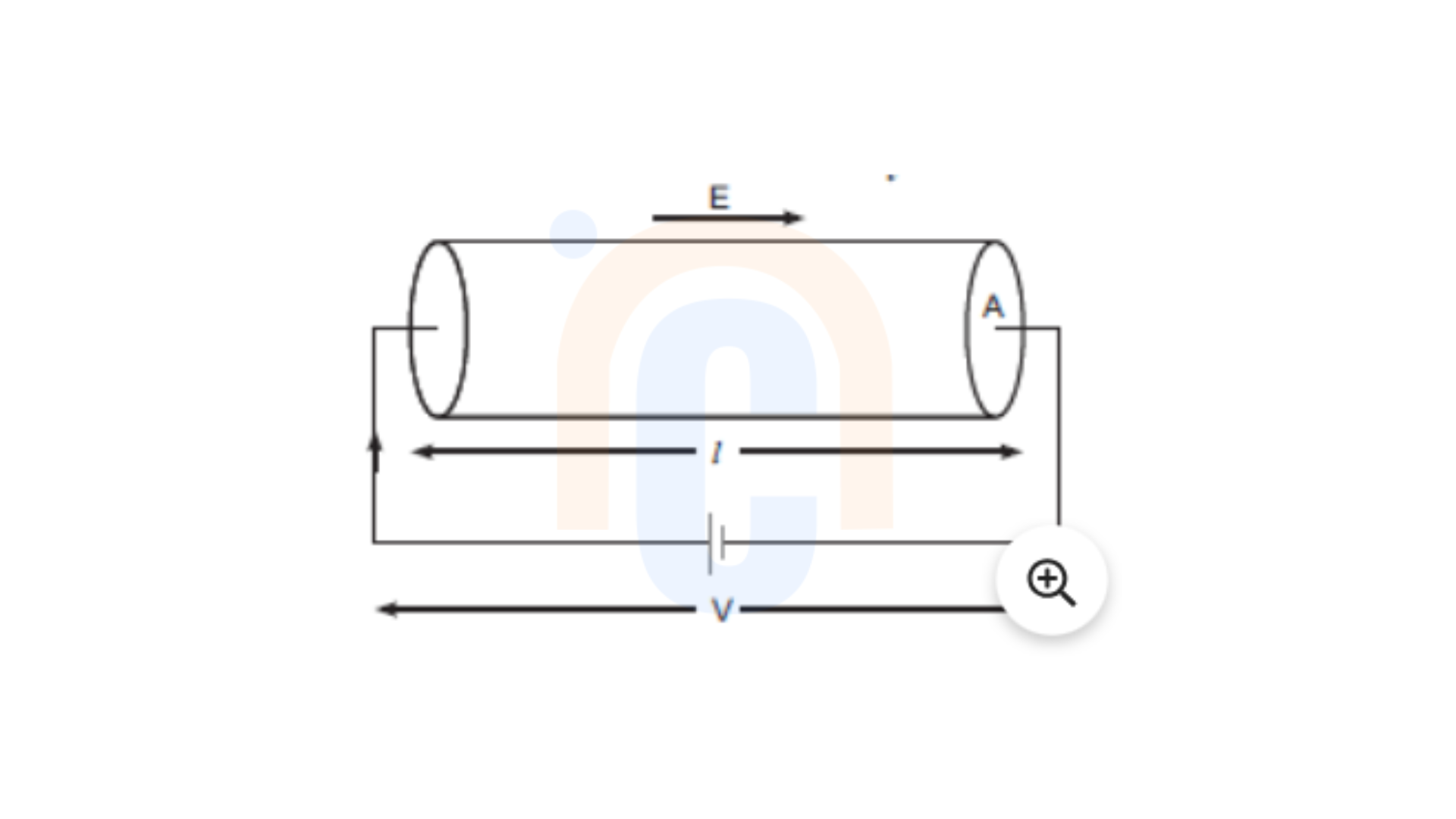
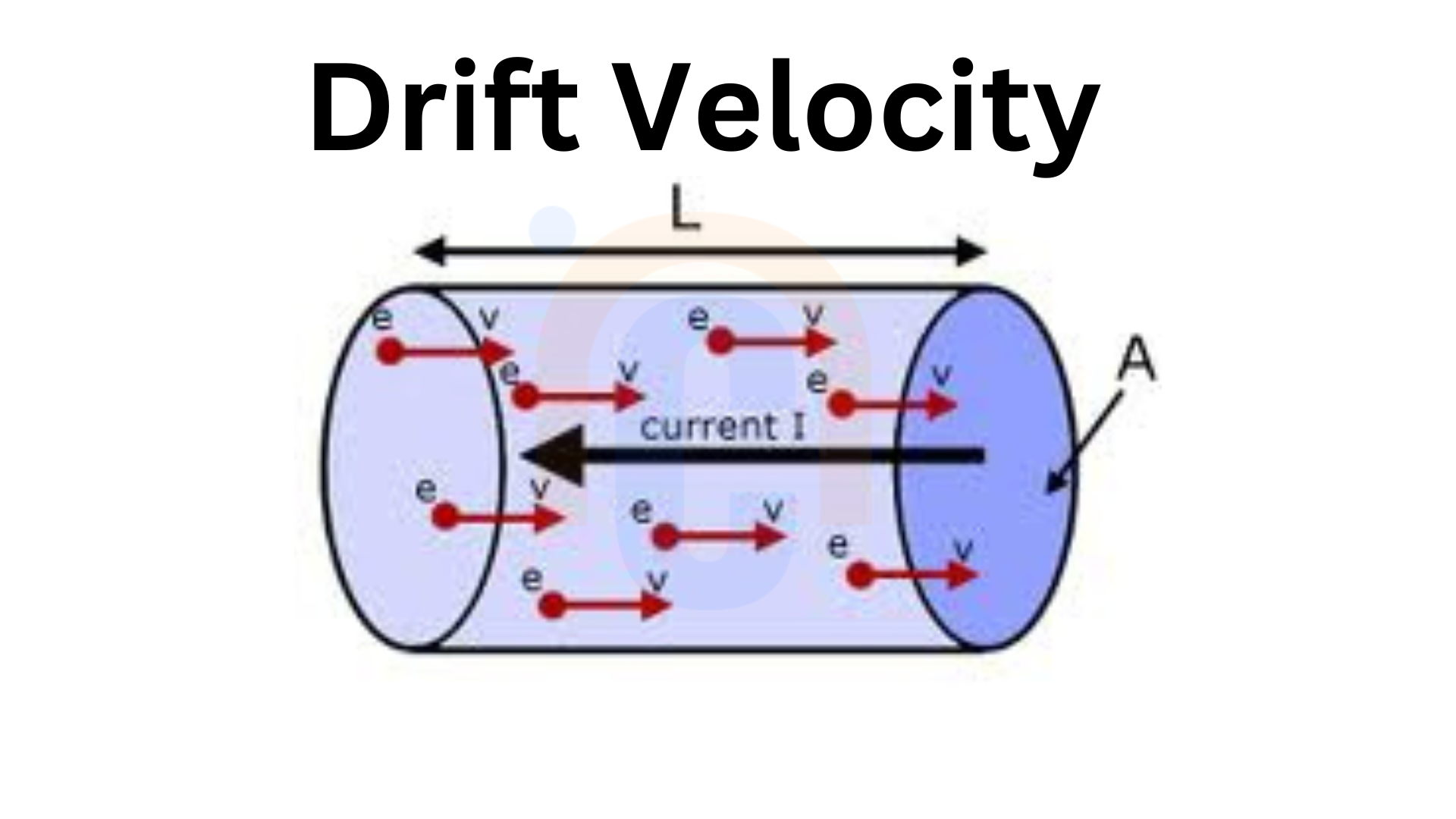
Consider a conductor having length l, area of cross section A and current density n.
Current flowing through the conductor is given by,
\(I=−neAv_d\)…(2)
Now, by substituting equation.(1) in equation.(2) we get,
\(I=neA\frac{eE}{m}τ\)\(∴I=\frac{ne^2AE}{m}τ\) …(3)
Electric field applied is given by,
\(E=\frac{V}{l}\) …(4)
Substituting equation. (3) in equation.(4) gives,
\(I=\frac{ne^2AVτ}{ml}\)Now, by rearranging the equation we get,
\(\frac{V}{I}=\frac{ml}{ne^2Aτ}\) …(5)
According to Ohm’s Law,
V=IR
Rearranging the above equation we get,
\(R=\frac{V}{I}\)Now, substituting the equation. (5) in above equation we get,
\(R=\frac{ml}{ne^2Aτ}\)Let ρ=\(\frac{m}{ne^2τ}\)
\(∴R=ρ\frac{l}{A}\)Where, ρ : Resistivity of the material
Thus, the formula for electrical resistivity is expressed as
\(ρ=\frac{m}{ne^2τ}\)
Note:
Electrical resistivity is inversely proportional to relaxation time. Reciprocal resistivity gives conductivity. It is denoted by σ. Therefore, \(σ=\frac{ne^2τ}{m}.\)
As the temperature of the conductor is reduced, the rate of electron collisions also diminishes. Consequently, the relaxation time increases. Thus, we can infer that relaxation time is affected by temperature.